Поскольку пл-ть А || пл-ти В и точки А1 и В1 принадлежат прямой РВ1, аналогично точк А2 и В2 принадлежат прямой РВ2, то прямая А1А2 || В1В2. Тогда РВ2 является секущей для параллельных прямых А1А2 и В1В2, тогда угол РА1А2 = углу РВ1В2 как соответственные. Аналогично РВ2 - секущая для параллельных прямых А1А2 и В1В2, тогда углы РА2 и РВ2 равны как соответственные, тогда треугольники РА1А2 и РВ1В2 подобны по трем углам (т.к. угол Р общий) и два других соответственно равны.
поскольку из условия дано что РА1/А1В1 = 3/2, то РВ1/РА1 = (РА1+А1В1)/РА1 = 5/3, тогда В1В2 = (РВ1/РА1) * А1А2 = (5/3) * 6 = 10 см
Дано: Решение: SABCD - правильная AB = BC = BS = 1 ΔSCD и ΔSAB - равносторонние SM = MC; SK = KB CD = AB и CM = KB; => DM⊥SC и AK⊥SB ----------------------------- Следовательно: AK = MD Доказать: AK = MD и трапеция AKMD - равнобедренная Найти: cos α
Построим SF⊥BC. Так как ΔBSC - равносторонний, то BF = FC = 0,5 Тогда: SF = √(SC²-FC²) = √0,75 = √3/2 и NF = SF/2 = √3/4
SX - высота пирамиды. В ΔSXF: ∠SXF = 90°; XF = 0,5; SF = √3/2 Тогда: SX = √(SF²-FX²) = √(0,75-0,5) = √0,25 = 0,5 и ΔSXF - равнобедренный, т.е. SX = XF = 0,5 и ∠SFX = 45°
В трапеции AKMD находим NP = MP':
так как KM = BC/2 по условию, то MN = BC/4 = 0,25 так как DM⊥SC и СМ = 0,5; DC = 1, то: DM = √(1-0,25) = √3/2 Тогда: NP = MP' = √(DM²-(PD-MN)²) = √(3/4 - (0,5-0,25)²) =√(11/16) = √11/4
СD = 7; -11
|CD| =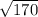
логически так