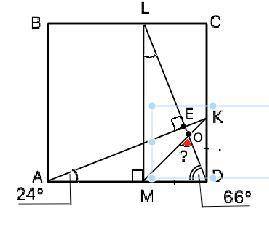
ответ: Угол DOM=69°
Объяснение: Сделаем рисунок. Обозначим точку пересечения АК и LD буквой Е и рассмотрим ∆ АЕД и ∆ LMD. Они прямоугольные ( DL перпендикулярна АК по условию) и имеют общий угол при вершине D. Он равен градусной мере развернутого угла без ∠DEA и без ∠ЕАD. Угол ЕDA= 90°-24°=66°. ⇒ ∠ МLD=∠КАD=24°
LM⊥AD (дано) ⇒ LМ║CD. ⇒ LМ=CD. Т.к. АВСD – квадрат, то LM=AD.
∆ АКD=∆ LDМ по катету ( LM=AD) и острому углу при вершине D. Поэтому KD=MD. Катеты прямоугольного треугольника АDМ равны. следовательно, его острые углы равны 45°. ⇒∠OMD=45°
Из суммы углов треугольника
Угол DOM=180°-∠ОМD-∠МDО=180°-45°-66°=69°
Через две параллельные прямые AA1 и BB1 проходит плоскость.
Плоскости AA1BB1 и p пересекаются по прямой A1B1.
Все общие точки двух плоскостей лежат на этой прямой.
Следовательно точка O лежит на прямой A1B1.
Диагонали трапеции AA1BB1 пересекаются в точке O.
S(BOA1) =S(B1OA) =5
(Это свойство трапеции. Треугольники BAA1 и B1AA1 имеют общее основание и равные высоты (расстояние между параллельными), следовательно их площади равны. Вычитаем общую площадь AOA1
=> S BOA1=S B1OA.)
Треугольники BOA1 и AOA1 имеют общую высоту, следовательно их площади относятся как основания, 1:2.
S(BOA1)/S(AOA1) =1/2 => S(AOA1) =5*2 =10
Аналогично
S(BOB1)/S(B1OA) =1/2 => S(BOB1) =5/2 =2,5
S(AA1BB1) =5 +5 +10 +2,5 =22,5

Объяснение:
На скриншоте. Большой треугольник каждая сторона из 2-х палочек и в нем маленький - перевернутый.