ответ:Первое-медиана делит основание треугольника на 2 равные части
Второе-образовались разные треугольники,не равные между собой,с разным периметром
Третье-периметр треугольника АВС без медианы равен 60см,
АD=DC
P=AB+BC+AD+DC
Периметр треугольника АВD
Р=АВ+АD+BD(медиана)
Периметр реугольника ВСD
P=BC+DC+BD(медиана)
периметры второго и третьего треугольника соответственно равны 36 и 50 см,у каждого из них одной из сторон является медиана
Узнаём,чему она равна
36+50=86 см-это периметры двух образовавшихся треугольников
В 86 см входят две медианы
(86-60):2=26:2=13 см
Одна медиана равна 13 см
Проверка
36-13=23 см(без медианы)
50-13=37 см(без медианы)
23+37=60 см(периметр треугольника АВС)
Объяснение:
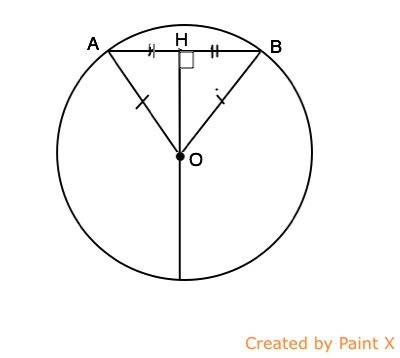
Соединим центр О окружности с концами хорды АВ. ОА=ОВ=R.
Треугольник АОВ - равнобедренный. Проведем высоту ОН этого треугольника.
Угол ОНВ=углу ОНА=90º
«Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один»
Следовательно, и к середине хорды можно провести только один перпендикуляр.
Высота ОН - медиана равнобедренного треугольника.
АН=ВН. Точка Н - середина АВ.
Следовательно, ОН, проходящий через середину АВ, есть срединный перпендикуляр хорды АВ, ч.т.д.
обозначим стороны треугольника, АС, СМ=СВ, АВ. АМ - медиана
АС+АВ+СМ+МВ=60
АС+СМ+АМ=36
АВ+ВМ+АМ=50
АС+СМ=36-АМ
АВ+ВМ=50-АМ
50-АМ+36-АМ=60
-2АМ=-26
АМ=13