Оба треугольника 1 и 2 подобны исходному. Если какая-то (все равно - какая) сторона треугольника z, а соответственные ей стороны треугольников 1 и 2 - x и y, то
x + y = z; (это справедливо для любой стороны, но видно лучше всего, если z - основание) или x/z + y/z = 1;
Если обозначить S площадь всего треугольника, то S₁/S = (x/z)^2 и S₂/S = (y/z)^2; (площади подобных фигур пропорциональны квадратам линейных размеров, ну, скажем к примеру, - если сторона квадрата в 2 раза больше, то площадь - в 4, и так для любых подобных фигур - это теория, должны знать :))
Поэтому √(S₁/S ) + √(S₂/S) = 1; или S = (√S₁ + √S₂)^2 = (4 + 5)^2 = 81;
Отсюда площадь параллелограмма равна S - (S₁ + S₂) = 81 - (16 + 25) = 40;
Дано: ABCD - параллелограмм. , AK=64 см, KD=225 cм,
, AK=64 см, KD=225 cм, 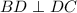 .
.
Найти: BD
Решение: Треугольник АВD является прямоугольным, так как BD перпендикулярно DC. A DC||AB. Значит BD является секущей при параллельных АВ и CD. Поэтому
Есть такое свойство в прямоугольном треугольнике, что высота, проведенная к гипотенузе, является средним геометрическим отрезков, на которое делит высота гипотенузу.
BK=120 см.
Теперь по теореме Пифагора BD - гипотенуза треугольника BKD.
ответ: BD=255 cм.