По свойству отрезков касательных, проведенных из одной точки к одной окружности МК=МN₁; NN₁=NE₁=12; EE₁=EK; где N₁ и E₁ - точки касания окружности с гипотенузой МN и катетом NЕ соответственно.
EK=ЕE₁ =ОК =х - радиус, подлежащий определению. Из данного в условии прямоугольного треугольника свяжем теоремой Пифагора гипотенузу и катеты. (МN=8+12=20; МЕ=8+х; NE=12+х)
МN²=МЕ²+NE²; 20²=(8+х)²+(12+х)²; 400=64+16х+х²+144+24х+х²;
2х²+40х-192=0, сократим на два обе части уравнения. х²+20х-96=0, ПО теореме, обратной теореме Виета х=-24- не подходит по смыслу задачи, не может радиус быть отрицательным. х=4
ответ Радиус равен 4см
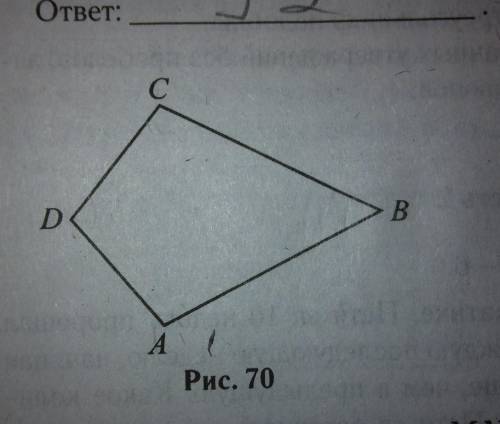
∠А=92°
Проведи прямую через точки В и Д.
Теперь рассмотрим два треугольника
ΔАВД и ΔСВД.
Так как АВ=ВС , АД=СД и ВД= общая сторона , то согласно 3-му признаку равенства треугольников (если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны) ΔАВД = ΔСВД.
Соответственно ∠С=∠А.
Сумма всех углов четырёхугольника равна 360°
∠А+∠В+ ∠С+∠Д=360°;
2∠А+76°+100°=360°
2∠А=360°-176°
∠А=184°:2
∠А=92°