
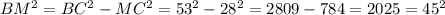 . ВМ=45.
. ВМ=45. , то отношение длин задает отношение центральных углов, которыми данные дуги определены, то есть один центральный угол будет равен 9х, а другой 11х. В сумме они дают 360 градусов, значит: 9х+11х=360, тогда 20х=360, х=18. Центральный угол, опирающийся на меньшую из дуг равен 9х=9*18=162 градуса.
, то отношение длин задает отношение центральных углов, которыми данные дуги определены, то есть один центральный угол будет равен 9х, а другой 11х. В сумме они дают 360 градусов, значит: 9х+11х=360, тогда 20х=360, х=18. Центральный угол, опирающийся на меньшую из дуг равен 9х=9*18=162 градуса.
Дано:
ABCD - параллелограмм
S(ABCD) = 256
AK = KD
-------------------------------------------
Найти:
S(AKCB) - ?
Мы знаем что площадь это трапеций будет так:
S(ABCD) = AD × h
Площадь трапеции равна полусумме оснований, умноженной на высоту. Выразим площадь трапеции через площадь параллелограмма:
S(ABCE) = 1/2 × (AE + BC)×h = 1/2 × (1/2 ×AD + AD)×h = 1/2 × 3/2 × AD × h = 3/4 × AD × h = 3/4 × S(ABCD) = 3/4 × 256 = 192
ответ: S(ABCE) = 192
Решено от: