
27 cм²
Объяснение:
Задание
Дана трапеция ABCD (AD || BC). Диагонали трапеции
пересекаются в точке 0, Ѕвос= 3 см², Scod = 6 см².
Найдите площадь трапеции ABCD.
Решение
1) Диагонали трапеции делят её на 4 треугольника, обладающих следующими свойствами:
а) треугольники, прилегающие к боковым сторонам трапеции, являются равновеликими;
б) квадрат площади треугольника, прилегающего к боковой стороне трапеции, равен произведению площадей треугольников, прилегающих к её основаниям.
2) Таким образом:
S abo = Scod = 6 см²
(S abo)² = Ѕвос · Ѕaod, откуда Ѕaod = 6² : 3 = 12 см².
3) S abсd = S abo + Ѕвос + Scod + Ѕaod = 6 + 3 + 6 + 12 = 27 cм²
ответ: 27 cм²
7 см.
Объяснение:
Первый решения:
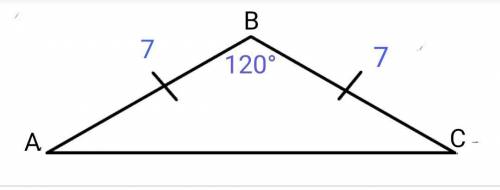
Для определённости допустим, что данный равнобедренный треугольник АВС имеет основание АС, АВ = ВС = 7 см, ∠ В = 120°.
По теореме R = a /(2•sinA).
В нашем случае R = АС /(2•sinВ).
1) По теореме косинусов
АС² = АВ² + ВС² - 2•АВ•ВС•cosB = 7² + 7² - 2•7•7•cos120° = 98 - 98•(-1/2) = 98 + 49 = 49•3.
AC = √(3•49) = 7√3 (см).
2) sin120° = sin60° = √3/2;
R = 7√3 /(2•√3/2) = 7√3/√3 = 7 (см).
Второй решения:
Второй решения:R = abc/(4S)
В первом решения найдено основание.
S = 1/2•AB•BC•sinB = 1/2•7•7• √3/2 = 49√3/4.
R = abc/(4S) = 7√3•7•7/(4•49√3/4) = 7•7•7/49= 7 (см).
Существуют и другие решения.
ответ: KD = 5 cm
Объяснение: