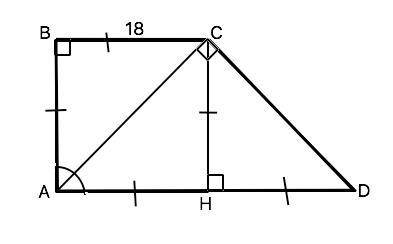
АВ⊥ВС, АВ⊥АD; АС - биссектриса прямого угла ВАD ⇒
∠ВАС=45°. Угол ВСА=∠САD ( накрестлежащий. ⇒ ∠ВАС=∠ВСА ⇒ треугольник АВС равнобедренный, его катеты АВ=ВС.
а) Высота прямоугольной трапеции равна его меньшей стороне, которая перпендикулярна основаниям. А т.к. АВ=ВС, то и высота СН=ВС
б) Противоположные стороны ☐АВСН равны и лежат на параллельных прямых, ⇒АН=ВС=18 см. Т.к. ∠АСD=90°( дано), а ∠САD=45°, отрезок СН=АВ и является высотой и медианой прямоугольного треугольника АСD, поэтому СН=НD=AH=18 см. Т.к. в прямоугольном треугольнике медиана равна половине гипотенузы, основание АD=2 CH=2•18=36 см
1) Проводим прямую ВЕ параллельную СD, получаем, что ВС=ЕD=10.
АЕ=AD-ED=20-10=10
2)В ΔАВЕ: АВ=6, ВЕ=8, АЕ=10, ВН-высота
3) р(полупериметр)=1/2*(АВ+ВЕ+АЕ)=12
4) S=√ (p(p-АВ)*(p-ВE)*(p-АE))=24
5) S=(1/2*ВН)/АЕ ⇒ ВН=2S/АЕ=4,8
ответ: 4,8.