Сейчас я попробую, что-нибудь решить.
Я же всё-таки не знаток, мне недавно 16 исполнилось.
S1(Площадь правильного треугольника)=корень из 3 делим на 4 и умножаем на сторону в квадрате=SQRT3/4*a*a
S2(площадь тетраэдра)=S1*4(так как в тетраэдре 4 равносторонних треугольника)=SQRT(3)*a*a=30*SQRT3
То есть a*a=30
а=SQRT(30)
h(высота)=SQRT6/3*a=4,4721...=4,47
Теперь найду основание конуса.
Радиус вписанной окружности равен.
r=a*SQRT3/6=1,5811=1,58
S3(Вся площадь конуса)=ПЛощади окружности + площади боковой стороны=r*r*П=7,85374999 + П*r*SQRT(r*r+h*h) =7,85 +23,55 =31,4 дм в квадрате
Я очень надеюсь, что правильно, заметь, конусы и тетраэдры я не проходил нигде, просто соображаю неплохо!!
Скажи
Сейчас я попробую, что-нибудь решить.
Я же всё-таки не знаток, мне недавно 16 исполнилось.
S1(Площадь правильного треугольника)=корень из 3 делим на 4 и умножаем на сторону в квадрате=SQRT3/4*a*a
S2(площадь тетраэдра)=S1*4(так как в тетраэдре 4 равносторонних треугольника)=SQRT(3)*a*a=30*SQRT3
То есть a*a=30
а=SQRT(30)
h(высота)=SQRT6/3*a=4,4721...=4,47
Теперь найду основание конуса.
Радиус вписанной окружности равен.
r=a*SQRT3/6=1,5811=1,58
S3(Вся площадь конуса)=ПЛощади окружности + площади боковой стороны=r*r*П=7,85374999 + П*r*SQRT(r*r+h*h) =7,85 +23,55 =31,4 дм в квадрате
Я очень надеюсь, что правильно, заметь, конусы и тетраэдры я не проходил нигде, просто соображаю неплохо!!
Скажи
242
Объяснение:
Площадь треугольника CDE равна половине произведения стороны CD на высоту, опущенную на неё из вершины E (обозначим её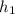 ). Тогда справедливо следующее равенство:
). Тогда справедливо следующее равенство:
Аналогично в треугольнике ABE:
Поскольку перескающиеся диагонали в трапеции отсекают подобные треугольники (ABE и CDE), найдём коэффициент подобия:
Поскольку в подобных треугольниках соответствующие элементы пропорциональны, то справделивы следующие соотношения:
Площадь трапеции ABCD равна произведению полусуммы её оснований (AB и CD) на высоту, которая равна сумме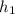 и
и 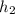 , то есть
, то есть