abc - равнобедренный треугольник, тк ав=ас=6. значит углы асв и авс равны между собой. найдём их: abc=acb = (180 - bac)/2 = (180-60)/2 = 60. то есть все углы у треугольника по 60. значит он равносторонний , и все стороны равны 6.
пусть точка e - середина bc. be=ec=3. найдём ае, который является и высотой и меридианой по теореме пифагора (если я не ошибаюсь с названием): ае = корень из (ас^2 - be^2) = корень из (36-9) = корень из (25) = 5.
теперь рассмотри треугольник dae. он прямоугольный (ad также перпендикулярно плоскости треугольника, как и bp. то есть ad образует прямой угол с любым отрезком или прямой, которые принадлежат плоскости треугольника. угол dae - прямой.)
опять же по теореме пифагора найдём гиппотенузу de:
de= корень из (ae^2 + da^2) = корень из (25+9) = корень из (36) = 6
ответ: de=6
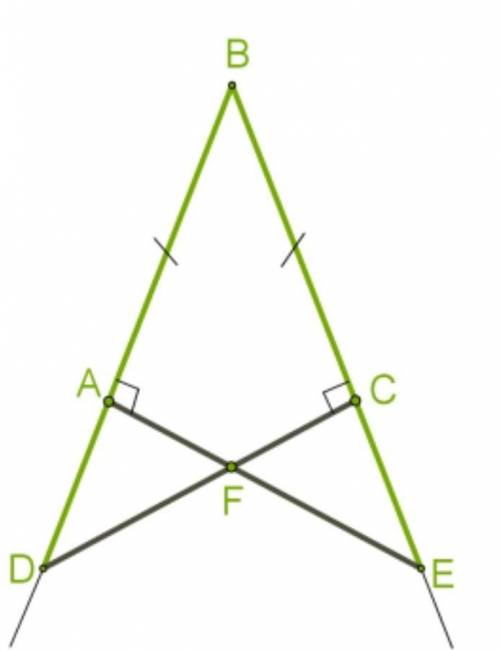
1. Назови треугольники, равенство которых позволит доказать равенство ΔAFD и ΔCFE:
ΔBAЕ = ΔBCD
По какому признаку доказывается это равенство?
По второму
Отметь элементы, равенство которых в этих треугольниках позволяет применять выбранный признак:
углы
∠CBD = ∠ABE
иначе, ∠В - общий для этих треугольников.
∠EAB = ∠DCB
По условию AE⊥ BD, CD⊥ BE, значит эти углы равны 90°.
стороны
BC = BA
По какому признаку доказывается равенство ΔAFD и ΔCFE?
По второму
Отметь элементы, равенство которых в треугольниках ΔAFD и ΔCFE позволяет применять выбранный признак:
углы
∠FAD = ∠FCE
так как эти углы прямые
∠CEF = ∠ADF
из равенства треугольников ΔBAЕ и ΔBCD.
стороны
AD = CE
AD = BD - BA, CE = BE - BC
BD = BE из равенства треугольников ΔBAЕ и ΔBCD, ВА = ВС по условию, значит AD = CE.
2. Величина угла, под которым перпендикуляр CD пересекает прямую BA — 71°
Угол, под которым CD пересекает ВА, - это ∠ADF.
Угол, под которым АЕ пересекает ВС, - это ∠СЕF, по условию ∠CEF = 71°.
∠ADF = ∠CEF = 71° из равенства треугольников AFD и CFE.