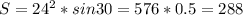Объяснение:
10)
Дано:
Прямоугольный треугольник
с=13см гипотенуза
а=12см катет
S=?
Решение
По теореме Пифагора найдем второй катет.
b=√(c²-a²)=√(13²-12²)=√(169-144)=√25=5см
S=1/2*a*b=1/2*5*12=30cм²
ответ: 30см²
1)
Дано:
Ромб
d1=6см диагональ
d2=14см диагональ
S=?
Решение
S=1/2*d1*d2=1/2*14*6=42см²
ответ: 42см²
2)
Дано:
Ромб
Р=96ед
<a=3°
S=?
Решение
Р=4а, где а-сторона ромба
а=Р/4=96/4=24ед сторона ромба
S=a²*sin<a=24²*1/2=288ед²
ответ: 288ед²
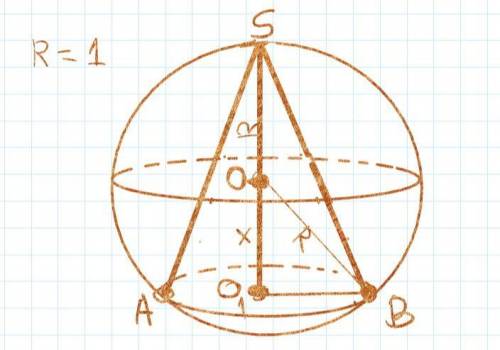
Пусть OO₁ = x (см. чертеж)
Из ΔOO₁B, используя теорему Пифагора, получаем:
O₁B² = 1 - x² (O₁B - радиус основания конуса)
SO₁ = 1 + x - высота конуса
Объем конуса вычисляется по формуле:
V = ⅓·πr²h, где r - радиус основания конуса, h - его высота
В нашем случае:
V(x) = ⅓·π·(1 - x²)(1 + x)
Исследуем на экстремум функцию f(x) = (1 - x²)(1 + x) = -x³ - x² + x + 1
f'(x) = -3x² - 2x + 1 = 0; Нули производной: -1; ⅓, причем x = ⅓ - максимум!
Таким образом для x>0 f(x) принимает наибольшее значение при x = ⅓, а значит и V(x) принимает наибольшее значение в этой же точке:
V(⅓) = ⅓·π·(1 - ⅑)(1 + ⅓) = 32/81 · π
6. DB = 13см
Объяснение:
#5
∆ЕОМ = ∆КОМ по 1 признаку (ЕО=ОК; ЕМ=КМ; <ЕОМ= <КОМ) => <ОМЕ = <КМО (как соответствующие элементы)
∆ЕСМ = ∆КСМ по 1 признаку (ЕМ=КМ; СМ- общая; <ЕМС = <КМС)
Что и требовалось доказать
#6
1) Из чертежа мы видим, что <ОАВ = <ОВА => ∆ОАВ - р/б => ОА=ОВ
Раз <САВ = <DBA и <ОАВ = <ОВА => <САО= <DBO
∆САО = ∆DBO по 2 признаку (АО=ОВ; <САО = <DBO; <СОА = <DOВ как вертикальные)
Что и требовалось доказать
2) Из доказанного выше: ∆САО = ∆DBO => CA=DB (как соответствующие элементы) => DB=13см
10) S=30 (см^2)
1) 42
2) 288
Объяснение:
10) Пусть другой катет - x. Найдем другой катет по теореме Пифагора:
Формула: площадь прямоугольника равна половине произведения катетов, т.е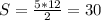 (см^2)
(см^2)
1) По формуле: площадь ромба равна половине произведения диагоналей: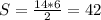
2) P ромба = 4 * сторона ромба, значит сторона ромба равна 96/4=24
По формуле: площадь ромба равна квадрату стороны, умноженному на синус угла, т.е