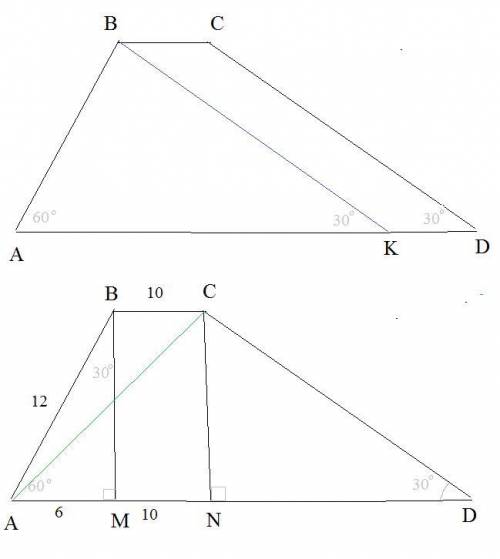
∠ВАD=60°
∠CDA=30°
BC=10 см
AD=34 cм
Сделаем дополнительное построение: проведем BK||CD.
Получим треугольник АВК с углами 60° и 30° ( соответственные углы при параллельных прямых и секущей равны)
Значит, Δ АВК - прямоугольный.
АК=AD-KD=AD-BC=34-10=24 см
Катет АВ против угла в 30 градусов равен половине гипотенузы АК
АВ=12 см
Проведем высоты ВМ и СN из вершин В и С на основание AD
AM=АВ/2 ( катет против угла в 30° в прямоугольном треугольнике АВМ)
АМ=6 см
BM=6√3 cм
MN=BC=10 см
AN=AM+MN=6+10=16 cм
СN=BM=6√3 cм
Из прямоугольного треугольника АСN:
AC²=AN²+CN²=16²+(6√3)²=256+108=364
АС=√364=2√91 cм
Площадь треугольника равна половине произведения его сторон на синус угла, заключенного между ними.
S = 1/2 РМ* MN * sin(120)
S = 1/2 3*4* √3/2=3√3
Но площадь треугольника равна и половине произведения его высоты на сторону, к которой она проведена.
S=ah:2
МН проведена к РК.
РК найдем по теореме косинусов:
PK² = 3² + 4² - 2*3*4*cos(120°) = 9 + 16 -24(-1/2)=37
PK=√37
МН=2 S:37=(6√3):√37 или
МН=10,3923:6,0827≈1,7 см