Путешествие во времени — гипотетическое перемещение человека или каких-либо объектов из настоящего в или будущее, в частности, с технического устройства, называемого «машиной времени».
Фотография 1941 года на открытии Голд-бридж в Британской Колумбии (Канада) запечатлела якобы путешественника во времени. В действительности, облик мужчины соответствует эпохе и отличается от собравшихся тем, что те одеты более официально. Очки «путешественника — хипстера» изобретены ещё в 1920-е годы, на футболке угадывается логотип «Монреаль Марунз»[1][2].
Объяснение:
вот все правильно
Задача: Знайти радіус кола, вписаного в рівносторонній трикутник, якщо радіус кола, описаного навколо цього трикутника, дорівнює 16 см.
Рішення:
Формула кола, вписаного в рівносторонній трикутник:
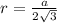 , де а — сторона правильного тр-ка
, де а — сторона правильного тр-ка
Знайдемо сторону а через формула кола, описаного навколо рівностороннього тр-ка:
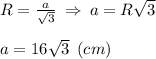
Підставимо значення у формулу кола, вписаного в рівносторонній тр-к

Відповідь: Радіус кола, вписаного в рівносторонній трикутник, рівний 8 см.
Задача: Точка перетину висот BK і PH трикутника BEP є центром вписаного в нього кола. Доведіть, що тр-к BEP рівносторонній.
Рішення:
Центром вписаного в коло трикутника є перетин бісектриса тр-ка, отже і BK та PH є бісектрисами. Висота є бісектрисою, якщо суміжні сторони рівні.
BK — висота/бісектриса ⇒ PB = EB;
PH — висота/бісектриса ⇒ PB = EP.
Відповідно, PB = EB = EP ⇒ ΔBEP — рівносторонній, що і потрібно було довести.
ответ: 4 см
Объяснение:
Пусть O и O1 - точка пересечения медиан или высот правильных треугольников-оснований ΔA1B1C1 и ΔABC в правильной усеченной треугольной пирамиде ABCA1B1C1.
Поскольку пирамида правильная, то если провести перпендикуляр к плоскости ABC через точку O, то она пересечет и точку O1, иначе говоря, OO1 - выcота пирамиды, а угол 60° между боковым ребром и основанием ABC является углом между AA1 и A1O1.
Как видим, задача нахождения высоты h эквивалентна нахождению высоты трапеции A1AOO1 с высотой AR (смотрите рисунок).
Поскольку треугольники оснований правильные, то длины их медиан равны: 2*√3/2 = √3 cм и 6*√3/2 = 3√3 см, а поскольку точка пересечения медиан делит медианы в отношении 2:1 cчитая от вершины, то
AO = 2√3/3 см; A101 =2√3 см
Откуда:
A1R = 2√3 - 2√3/3 = 4√3/3 см
Таким образом:
h = A1Rtg(60°) = 4√3/3 * √3 = 4 см