
ответ:В данной задаче фонарь, который висит на высоте 3,5 метра является катетом прямоугольного треугольника. Сумма расстояния человека и его тени является вторым катетом.
Запишем длину тени как х.
В таком случае получим: 12 + х.
Для второго треугольника рост человека является первым катетом, а его тень вторым.
Получаем два подобных треугольника.
Составим пропорцию.
1,5 / 3,5 = х / х + 12.
Умножаем между собой крайние члены пропорции.
1,5 * х + 18 = 3,5 * х.
2 * х = 18.
х = 18 / 2.
х = 9 метров.
Длина тени человека 9 метров.
Объяснение:
Точка пересечения диагоналей квадрата является центром квадрата. Т.к. из него проведена перпендикулярная прямая, значит расстояние от т. О до вершин квадрата будет одинаковое. Следовательно, нам нужно найти одно такое расстояние, чтобы знать все.
Стороны квадрата (а) равны. Диагонали у квадрата равные (d), и точк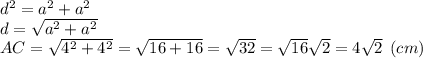 а пересечения делит их пополам.
а пересечения делит их пополам.
Р-м ΔAOM:
∠O = 90°, AO — половина диагонали, OM — перпендикуляр к плоскости квадрата. АМ — наклонная.
AO = d/2
Ищем, чему равна диагональ квадрата:
AO = (4√2)/2 = 2√2 см
Теперь можем найти длину отрезка AM
ответ: Расстояние равно √33 см, или приблизительно 5,74 см.