Объем пирамиды равен одной трети произведения ее высоты на площадь основания.
V=⅓ S∙h
Основание правильного шестиугольника состоит из шести правильных треугольников.
Площадь правильного треугольника находят по формуле:
S=(а²√3):4
S=4√3):4=√3
Площадь правильного шестиугольника в основании пирамиды:
S=6√3
Высоту найдем из прямоугольного треугольника АВО:
Так как ребро образует с с диагональю основания угол 60°, высота пирамиды ВО равна
H=ВО=2:ctg (60°)= 2·1/√3=2√3
Можно найти высоту и по т. Пифагора с тем же результатом.
V= 2√3∙6 √3:3=12 (кубических единиц)
Подробнее - на -
Объяснение:
ответ: 8.5
Объяснение:
Заметим, что точка не лежит между двумя параллельными прямыми, а значит, фигура которая высекается прямыми будет трапецией в плоскости АD1D2, так как прямые параллельны. Посмотрим на рисунок в плоскости АD1D2 - это, как уже было сказано ранее, трапеция, но не простая. Известно равенство отрезков KC1 = C1D1. Рассмотрим ΔD1D2K.
В нем проведена прямая С1С2 ║основанию через середину стороны D1K(KC1 = C1D1), значит эта прямая - средняя линия треугольника ⇒точка C2 делит сторону пополам и, по свойству средней линии,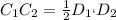 . Находим по этой формуле C1C2. Он равен 8.5.
. Находим по этой формуле C1C2. Он равен 8.5.