1. llanach w NBAD наклонные к плоскокти а, ме - ер- nerup BC-50% -7 cm mare pe para a) BCCM 6) MC MD MCMB MB MD ! bal 2. Orona povoro aparentera CTCP угольник с идмерения 9 см и 12 см, а диагональ параллелерін exa para 7 em Hanume pere sepene napake termen 3. Стороны прямоугольника ABCD равны 7 см и 23 см. К плоскости прямо- уальника через точку пересечения его диагоналей проведен перпендикуляр Spannun 7 cm Haxure yma e прямой SA и помкостью прымоуполь Ka ABCD 4. B peyroamere MNK MN-10 cm, NK 17 cm, MK-21 cm. Ma pep шины Мк его плоскости проведен перпендикуляр MP, рапии 15 см. Найдите расстояние от очки Рдо стороны MA. 5. В треугольной пирамиде SABC с вершиной Ѕ боковые ребра nouapuo neputankapuu, SASM, SB-9cm SC-12 cm. Han mere matreue xeyrpamoro yra, oppuamaro ROCKORTASBO HABC
відповідь:
пояснення:
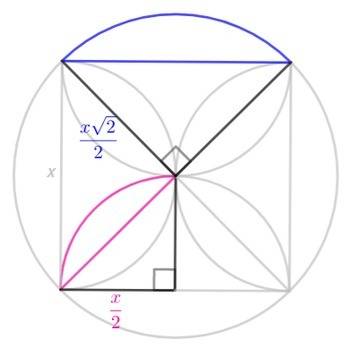
проекция вершины s на основание , есть точка пересечения диагоналей квадрата abcd .
положим что это точка h .
l,k середины as, cs соответсвенно , также положим что b1k пересекает bc в точке x , можно теореме менелая , тогда
bb1/b1s * sk/kc * cx/bx=1
или (20-5)/5*(1/1)* (cx/(24+cx))=1 , откуда cx=12 , значит bx=36. аналогично если y точка пересечения lb1 с ab , тогда by=36 .
опустим высоту из точки b1 на основание , основание высоты n будет лежат на диагонали . найдём b1n , подобия треугольников shb и b1nb , тогда sh/b1n = 4/3
по теореме пифагора sh=sqrt(bs^2 - bh^2) = sqrt(bs^2-(bd/2)^2) = sqrt(20^2-(12 sqrt()= sqrt(112) , значит b1n = 3*sqrt(7) и bn=sqrt(15^2-9*7)=9*sqrt(2) . xby равнобедренный и прямоугольный треугольник , положим что m точка пересечения bn и xy , тогда bm=36*sqrt(2) , и mn=bm-bn= 36*sqrt(2)-9*sqrt(2) = 27*sqrt(2) .
тогда если "a" это угол между плослкостью основания и данной плосокостью то
tga=b1n/mn = 3*sqrt(7) / 27*sqrt(2) = sqrt(14)/18 , откуда
a=arctg(sqrt(14)/18) .