14 2/3 π cм
Объяснение:
1) В четырёхугольнике, образованном углом 40°, двумя углами каждый по 90° (углы между радиусами окружности и касательными), четвертый угол (между двумя радиусами, перпендикулярными к касательным) равен:
360° - 40° - 90° - 90° = 360° - 220° = 140° - центральный угол, опирающийся на меньшую дугу.
2) Находим градусную меру большей дуги:
360° - 140° = 220°.
3) Длина окружности радиуса R = 12 см равна:
L = 2πR = 2π · 12 = 24π
4) Длина большей дуги:
L₁ = 24π · (220/360) = 14 2/3 π cм ≈ 46,05 см
ответ: 14 2/3 π cм
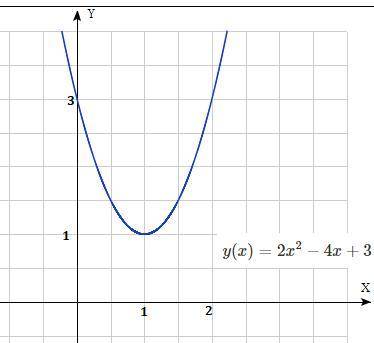
у=2х²-4х+3 . 1)Найдите точки пересечения графика с осью OY
2)Обоснуйте свой ответ, разрезав ось OX графика ( НЕ ЗНАЮ КАК ...)
3)Напишите уравнение оси симметрии ; 4)Постройте график.
Объяснение:
1) Область определения :х-любое ;
2) Это парабола ,ветви вверх . Координаты вершины
х₀=-в/2а, х₀=-(-4)/4= 1 , у₀=2*1²-4*1+3=3 , ( 1; 3). Ось симметрии х=1.
3) Точки пересечения с осью ох( у=0)
2x²- 4x+3=0 , Д=-8 , точек пересечения нет с ох нет.
4)Точки пересечения с оу ( х=0)
у(0)=2*0²-4*0+3=3 , Точка (0; 3).
5) Промежутки знакопостоянства функции : у>0 при х-любом
6) Функция убывает при х≤ 1 ,
функция возрастает при x≥1;
7) Наименьшее значение функции у=3 ( при х=1)
Наибольшего значения нет.
8)Множество значений функции у∈[3; +∞) ;
9)График функции ,
Доп. точки у=х²-4х+3
х: 2 3
у: 3 9
РИСУЕМ ПАРАЛЛЕРОГРАММ
РИСУЕМ ПРЯМЫЕ АА1 И СС1
ПО УСЛОВИЮ ОНИ ПАРАЛЛЕЛЬНЫ
СОЕДИНЯЕМ А1 И D С1 И В
У НАС ПОЛУЧАЮТСЯ ТРЕУГОЛЬНИКИ
НУЖНО ДОКАЗАТЬ ЧТО ИХ ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫ
ДЛЯ ТОГО ЧТОБЫ ЗАДАТЬ ПЛОСКОСТЬ НАМ НЕОБХОДИМО 3 ТОЧКИ
ЭТО БУДУТ ВЕРШИНЫ НАШИХ ТРЕУГОЛЬНИКОВ
ПОСКОЛЬКУ ПРЯМЫЕ АА1 И СС1 ПАРАЛЛЕЛЬНЫ И ВС И AD ТОЖЕ ПАРАЛЛЕЛЬНЫ(ТАК КАК ФИГУРА ПАРАЛЛЕРОГРАМ ПО ЕГО СВОИСТВУ)
ЕСЛИ ДВЕ ПРЯМЫЕ ОДНОЙ ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫ ТО ЭТИ ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫ.
2 ЗАДАЧА
РИСУЕМ ДВА ПАРАЛЛЕРОГРАММА РАЗ ОНИ НЕ ЛЕЖАТ В ОДНОЙ ПЛОСКОСТИ ЗНАЧИТ НЕ ПЕРЕСЕКАЮТСЯ ЗНАЧИТ ПАРАЛЛЕЛЬНЫ
ЕСЛИ СОЕДЕНИТЬ ВСЕ ВЕРШИНЫ АА1 ВВ1 СС DD1 ТО У НАС ПОЛУЧИТЬСЯ ПАРАЛЛЕЛЕПИПЕД
ПРОТИВОПОЛОЖЕННЫЕ ГРАНИ ПАРАЛЕЛЕПИПЕДА ПАРАЛЛЕЛЬНЫ
СЛЕДОВАТЕЛЬНО ПЛОСКОСТЬ СС1В1В ПАРАЛЛЕЛЬНА ПЛОСКОСТИ АА1DD1
ЧТО И ТРЕБОВАЛОСЬ ДОКАЗАТЬ.