1) Треугольники вне восьмиугольника равны по двум сторонам и углу между ними(по свойству правильного многоугольника), значит стороны вписанного многоугольника равны, а т.к. его стороны равны, то это правильный восьмиугольник.
2)В треугольнике АВМ:АД-высота(т.к.угол АДМ=90), также АД является медианой этого треугольника(ВД=МД по условию) из этого следует, что треугольник АВМ-равнобедренный. Тогда АВ=АМ=4. И т.к. АМ=МС, АС=АМ+МС=4+4=8.
3)Треугольники вне восьмиугольника равны по двум сторонам и углу между ними(по свойству правильного многоугольника), значит стороны вписанного четырехугольника равны, и это значит, что это четырехугольник-ромб, т.к. диагонали правильного восьмиугольника равны, то и в ромбе диагонали равны, из чего следует, что это квадрат.
4)Обозначим СД=х.Проведем высоты ВН1 и СН2, угол ДСН2=90-60=30. Тогда ДН2=1/2 СД=х/2. Т.к. АД=2х, то АН1=2х-х-х/2=х/2, из этого следует, что трапеция равнобедренная, а значит СД=2. Тогда АД=2СД=2*2=4. СН2=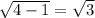
. S=СН2*АД=корень из 3*4=4 корня из 3
радиус вписанной окружности r = S / p = 2S / P, P---периметр
S(ABC) = AC*BC/2
tg(ABC) = AC/BC => AC = 2.4*BC
AB^2 = AC^2 + BC^2 = (2.4*BC)^2 + BC^2 = BC^2*(2.4*2.4+1) = 6.76*BC^2
AB = 2.6*BC
P(ABC) = AB+AC+BC = 2.6*BC+2.4*BC+BC = 6*BC
r = AC*BC / 6*BC = AC/6
аналогично для треугольника ACP:
треугольники АВС и АРС подобны (они прямоугольные, угол А ---общий) =>
угол АСР = углу АВС => tg(ABC) = tg(АCР) = АP/СP => АP = 2.4*СP
AС^2 = CР^2 + АР^2 = CР^2 + (2.4*СP)^2 = CР^2*(2.4*2.4+1) = 6.76*CР^2
AС = 2.6*CР
S(ACP) = CP*AP/2
r(ACP) = 12 = CP*AP/(AC+CP+AP)
CP*AP = 12(AC+CP+AP)
СР*2.4*СP = 12(2.6*CР+СР+2.4*СP)
СР*2.4*СP = 12*6*CР
СР = 12*6/2.4 = 30
АС = 2.6*30
r = AC/6 = 2.6*30/6 = 2.6*5 = 13