1. Найти угол между векторами AС и АB.

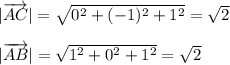
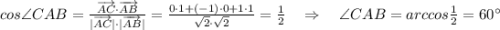
*Можно искать не косинус угла, а найти длину вектора BC, тогда ΔABC -- равносторонний и углы равны по 60°.
2. Найти координаты центра сферы и длину ее радиуса. Найти значение m.
Приведём уравнение к общему виду (x - x₀)² + (y - y₀)² + (z - z₀)² = R²:
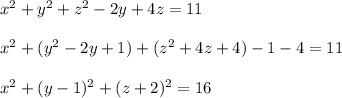
Тогда O (x₀; y₀; z₀) -- центр сферы, O (0; 1; -2),
R² = 16 ⇒ R = 4
Если точка принадлежит сфере, то подставив её координаты в уравнение, получится верное равенство. Подставим точки A и B в уравнение сферы:
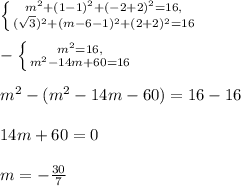
3. Найти уравнение плоскости α.
Ax + By + Cy + D = 0 -- общее уравнение плоскости.
n = (A; B; C) -- вектор нормали ⇒ A = 1, B = 2, C = 3, тогда

Если точка принадлежит плоскости, то подставив её координаты в уравнение, получится верное равенство:
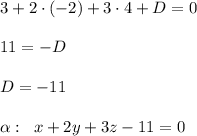
4. Найти общее уравнение прямой.
Общее уравнение прямой представляет собой систему уравнений двух пересекающихся плоскостей. Решение этой системы есть пересечение плоскостей, то есть прямая.
Зададим прямую параметрически:
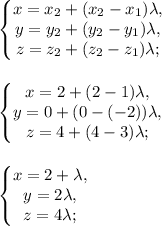
Исключим параметр λ:
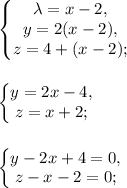
Последняя система -- это общее уравнение прямой.
Cоставим сначала уравнение плоскости, проходящей через ось ОУ и точку М(5,3,2).
Так как ось ОУ принадлежит искомой плоскости α, то любая точка, лежащая на оси ОУ, принадлежит плоскости α . В том числе и начало координат, точка О(0,0,0) ∈α .
Так как точка М(5,3,2)∈α , то и вектор ОМ∈α . Координаты вектора ОМ=(5,3,2) .
Также единичный вектор оси ОУ, вектор j=(0,1,0) , принадлежит плоскости α .
Можем записать нормальный вектор искомой плоскости α как векторное произведение векторов ОМ и j .
![\vec{n}=\Big [\, \overline {OM}\, ,\; \vec{j}\, \Big ]=\left|\begin{array}{ccc}\vec{i}&\vec{j}&\vec{k}\\5&3&2\\0&1&0\end{array}\right|=-2\vec{i}+5\vec{k}\\\\\\\lambda =-1\; \; \Rightarrow \; \; \; \; \vec{n}_1=\lambda \vec{n}=(2,0,-5)\\\\\alpha :\; \; A(x-x_0)+B(y-y_0)+C(z-z_0)=0\\\\2\cdot (x-5)+0\cdot (y-3)-5\cdot (z-2)=0\\\\\boxed {\alpha :\; \; 2x-5z=0}](/tpl/images/1007/7246/0300b.png)
Общие уравнения прямой, образованной пересечением двух заданных плоскостей имеют вид:
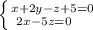
ответ: 324 см²
Объяснение:
Данный угол при вершине равнобедренного треугольника, иначе углы при основании, они равны, в сумме составят 120°*2=240°, чего быть не может. т.к. сумма углов треугольника равна 180°, если бы сторона в 14 см была бы боковой в этом треугольника, то сумма двух боковых 14+14 должна быть больше третьей, по неравенству треугольника, но
14+14=28/см/, а 28 см меньше 36 см. Значит, боковой стороной является сторона в 36 см. и тогда площадь равна 36*36*sin120°/2=36*36*0.5/2=324/cм²/