Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Пусть дан отрезок ВС.
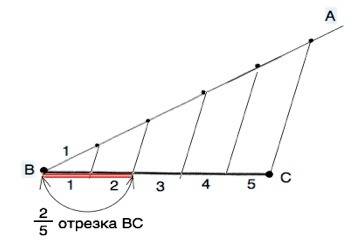
От конца В отрезка начертить луч и на нем от В отметить через равные промежутки 5 точек. Из пятой точки провести прямую через т.С отрезка ВС и провести параллельно ей прямые, пересекающие отрезок ВС. Этими прямыми ВС будет разделен на 5 равных частей. Любые две соседние части равны 2/5 исходного отрезка ВС.
пусть радиус описанной окр. вокруг АВС будет R1=5
а вокруг АОВ R2=5√2
во-первых , ∠АОВ=90+С/2 (это можно доказать путем нехитрых вычислений)
по теореме синусов в треуг. АВС АВ/sinC=2R1 AB=10sinC
AB=10*2sin(C/2)*cos(C/2)
в треуг АОВ AB/sin ∠AOB=2R2
AB=10√2*sin(90+C/2)
AB=10√2*cos(C/2)
приравниваем, сокращаем, выносим за скобки и получаем
cos(C/2)*(√2sin(C/2)-1)=0
cos(C/2)=0 √2sin(C/2)-1=0
С=180(либо 0) -не подходит С=90°
ответ : 90°