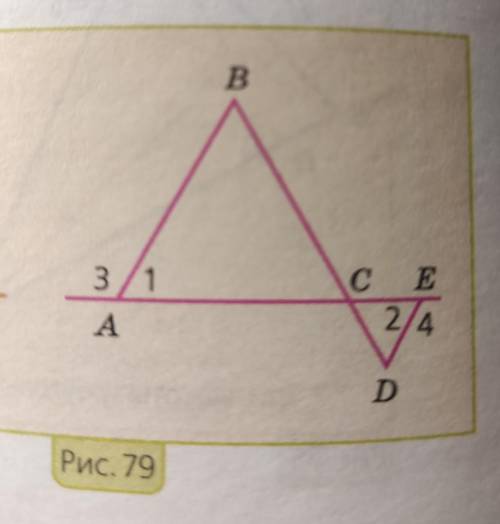
Так как внешние углы ∠3=∠4, то и внутренние углы смежных пар углов тоже равны, т.е. ∠1=∠2, углы АСВ и DCE равны как вертикальные, тогда т.к. СD=DE, угол 2 и угол 1 и угол DCE, и угол, вертикальный углу DCE, будут равны, т.е. получаем по признаку равнобедренного треугольника АВС - равнобедренный с основанием АС, значит, АВ=ВС. Доказано.
Через вершину конуса проведена плоскость под углом альфа к плоскости основания. Эта плоскость пересекает основание конуса по морде, которая видна из центра его основания под углом бета. Радиус основания R. Найдите площадь сечения.
Объяснение:
Образующие конуса равны , поэтому ΔABS равнобедренный. Пусть SK⊥AB, тогда ОК⊥АВ по т. О трех перпендикулярах.Т.к. ОА=ОВ как радиусы, то высота КО является биссектрисой ∠АОК=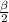
.
ΔАОК- прямоугольный ,
cos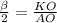
, KO=R*cos;
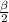sin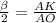
,AK=R*sin 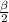,AB=α2Rsin .
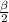ΔSKO прямоугольный ,cos α=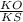
, KS=R*cos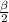/cosα.
S=0,5*AB*SK ,S=0,5*2R*sin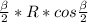
/ cosα,
S=0,5*R²*sinβ/cosα=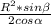
Площадь треугольника можно вычислить как половину произведения двух сторон на синус угла между ними:
S=\frac{1}{2}ab*sin \alphaS=21ab∗sinα
1) а=2 см, b= 3 cм, α=30°
S=\frac{1}{2}*2*3*sin30^o=3*\frac{1}{2}=\frac{3}{2}=1.5S=21∗2∗3∗sin30o=3∗21=23=1.5
ответ: SΔ=1.5 cм².
2) а=2√(2dm), b= 5√(dm), α=45°
S=\frac{1}{2}*2\sqrt{2dm} *5\sqrt{dm} *sin45^o=\sqrt{2}*\sqrt{dm}*\sqrt{dm}*5*\frac{\sqrt{2}}{2}=\frac{5\sqrt{2}\sqrt{2}}{2}dm=5dmS=21∗22dm∗5dm∗sin45o=2∗dm∗dm∗5∗22=2522dm=5dm
ответ: SΔ=5dm кв.ед.
3) а=2 м, b=√3 м, α=90°
S=\frac{1}{2}*2*\sqrt{3}*sin90^o=\sqrt{3}*1=\sqrt{3}S=21∗2∗3∗sin90o=3∗1=3
ответ: SΔ=√3 м².
4) а=0,4 см; b=0,8 см; α=60°
S=\frac{1}{2}*0,4*0,8*sin60^o=0,2*0,8*\frac{\sqrt{3}}{2}=0,1*0,8*\sqrt{3}=0,08\sqrt{3}S=21∗0,4∗0,8∗sin60o=0,2∗0,8∗23=0,1∗0,8∗3=0,083
ответ: SΔ=0,08√3 см²
1=54 градуса 2=76 градусов