
10. S=ah
BC=AD=20
ΔABE прямоугольный
∠А=30° т.к сумма углов вΔ=180°
катет лежащий напротив ∠=30° равен половине гипотенузы
BE=16÷2=8
S=8*20=160
11. CD=AB=8
∠MBA=30° т.к сумма ∠ вΔ=180°
катет лежащий напротив угла =30° равен половине гипотинузы
АМ=8÷2=4 АМ- высота
S=ah
S=10*4=40
Объяснение:
Медиана делит основание треугольника на две равные части,поэтому треугольники АВК и ВКС равны между собой по третьему признаку равенства треугольников-если три стороны одного треугольника равны трём сторонам другого треугольника,то эти треугольники равны между собой
АВ=ВС,как стороны равнобедреного треугольника
АК=КС ,сторону АС медиана поделила на две равных стороны
И ВК-общая сторона
Периметр АВС
АВ+ВС+АК+КС=36 см
Периметры двух треугольников АВК и ВКС равны
АВ+ВС+АК+КС+(ВК)+(ВК)+30+30=60 см
(60-36);2=24:2=12 см
Объяснение:
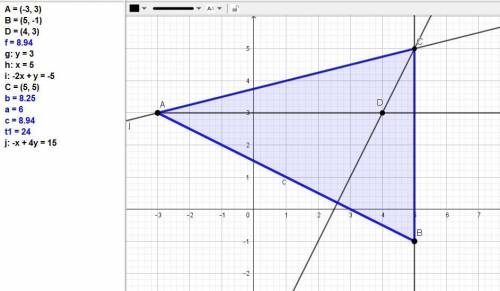
Уравнение АВ: (x-(-3))/(5-(-3) = (y-3)/(-1-3) или (x + 3)/8 = (y - 3)/(-4).
В общем виде x + 2y - 3 = 0.
Так как высота АД - горизонтальная линия, то уравнение стороны ВС:
х = 5.
В уравнении высоты СД как перпендикуляра к АВ коэффициенты А и В меняются на -В и А (скалярное произведение равно 0).
Уравнение СД: -2х + у + С = 0. Подставим координаты точки Д, через которую проходит высота: -2*4 + 1*3 + С = 0, отсюда С = 8-3 = 5.
Уравнение СД: -2х + у + 5 = 0.
Находим координаты точки С как точки пересечения стороны ВС и высоты СД:
{x = 5,
{-2х + у + 5 = 0, подставим х = 5.
-2*5 + у + 5 = 0, у = 10 - 5 = 5.
Точка С(5;5).
Уравнение АС: (x-(-3))/(5-(-3) = (y-3)/(5-3) или (x + 3)/8 = (y - 3)/2.
В общем виде x - 4y + 15 = 0.
10. Берём треугольник ABE. <A=30° (180-90-60), значит BE=1/2AB
Т.к. катет, лежащий напротив угла в 30°, равен 1/2 гипотенузы.
Значит BE=8
BC=AD по свой-вам параллелограмма, значит AD=20
Дальше формула площади параллелограмма.
a=AD
h=EB
Sпараллел.=20×8=160см²
11. Тоже самое. <B=30° (180-90-60), значит MA=1/2 гипотенузы. Гипотенуза = BA, а BA=CD (по свойствам параллелограмма)
BA=8 см
Значит 8:2=4
MA=4 см
AD=BC(по свойствам) =10
Та же формула. AD×MA
Sпараллел=10×4=40см²