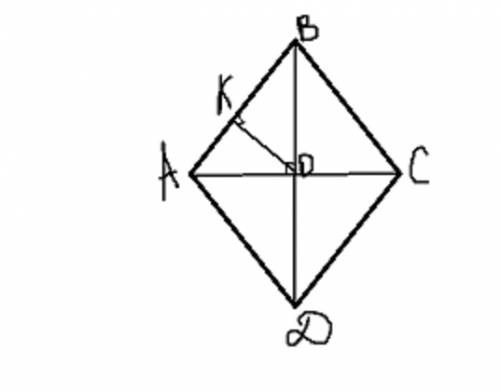
1) Рассмотрим треугольник АОВ прямоугольный
(т.к. по свойству ромба диагонали пересекаются под прямым углом)
Высота, выходящая из прямого угла треугольника, делит этот треугольник на подобные треугольники!
следует треугольник ОКВ подобен АОВ! следует КВ/OB=OK/OA
(OB=OД=8),
мы можем найти KB из треугольника OKB (по т.Пифагора)
KB"2=64-48=16; KB=4
(подставим все значения и найдём OA):
4/8=4 корня из 3/OA
ОА = 4 корня из 3*8/4=8 корней из 3
AC=2AO=16 корням из 3
из треугольника АОВ найдём AB = корень из (64+192)=корень из 256 = 16
1) Рассмотрим треугольник АОВ прямоугольный
(т.к. по свойству ромба диагонали пересекаются под прямым углом)
Высота, выходящая из прямого угла треугольника, делит этот треугольник на подобные треугольники!
следует треугольник ОКВ подобен АОВ! следует КВ/OB=OK/OA
(OB=OД=8),
мы можем найти KB из треугольника OKB (по т.Пифагора)
KB"2=64-48=16; KB=4
(подставим все значения и найдём OA):
4/8=4 корня из 3/OA
ОА = 4 корня из 3*8/4=8 корней из 3
AC=2AO=16 корням из 3
из треугольника АОВ найдём AB = корень из (64+192)=корень из 256 = 16

Известная диагональ делит 4-угольник на 2 пары равных треугольников по трём сторонам => соответственные углы у треугольников равны.
Вторая диагональ делит эти пары равных треугольников тоже на соответственно треугольники, которые равны уже по двум сторонам (стороне 4-угольника и части диагонали) и углу между ними => соответствующие части второй диагонали в 4-угольниках равны.
Взял с mail'ответы
лучший ответ