Площадь прямоугольника равна 300 см2.
Объяснение:
Так как периметр прямоугольника равен 70, то сумма смежных сторон равна 35.
Пусть 
, 
; 
.
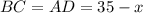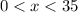Тогда по теореме Пифагора из треугольника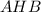 
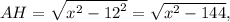
а из треугольника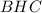 
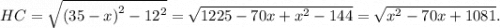
Так как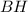 
— высота прямоугольного треугольника, проведенная к гипотенузе, ее можно выразить по формуле
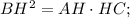
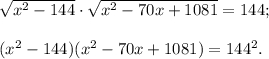
Разложим каждый из трехчленов на множители. Для первого это легко сделать по формуле разности квадратов
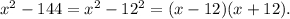
Корни второго найдем через дискриминант:
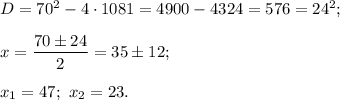
Тогда по формуле
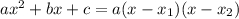
получаем, что
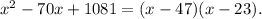
Значит уравнение перепишется в таком виде:
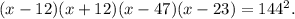
Перегруппируем сомножители:
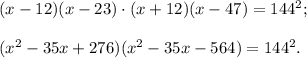
Сделаем замену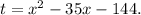 
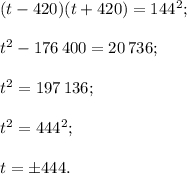
Делая обратную замену, получаем два случая.
1) 
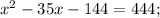
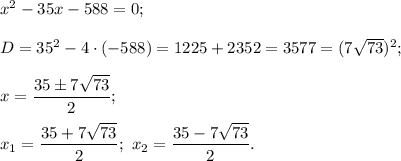
Оценим второй получившийся корень:
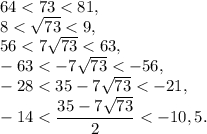
Получили 
, что противоречит смыслу задачи, следовательно,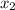 
— посторонний корень.
Аналогично
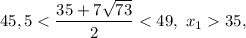
значит корень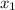 
также посторонний.
2) 
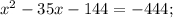
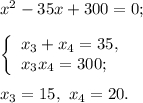
Оба этих корня подходят: при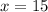 
значение 
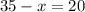и наоборот.
Таким образом, площадь прямоугольника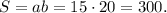 
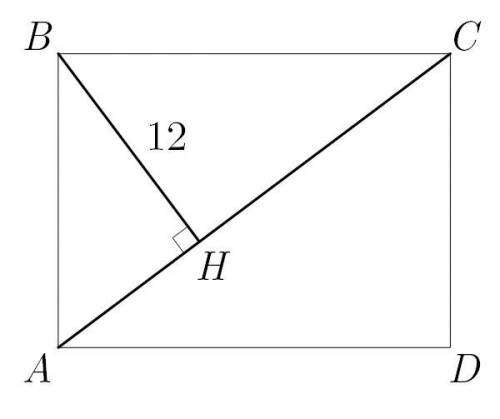
Пусть ABC - равнобедренный
∟B = 120 °, АС = 18 см, АК - высота.
В ΔАВС проведем высоту BD к основанию АС.
По свойству равнобедренного треугольника BD - биссектриса и медиана
AD = DC = 1 / 2AC = 18: 2 = 9 (см) (BD - медиана).
∟AВD = ∟DBC = 1 / 2∟В = 120 °: 2 = 60 ° (BD - биссектриса).
Рассмотрим ΔABD - прямоугольный (∟D = 90 °, BD - высота):
∟BAD + ∟ABD = 90 °; ∟BAD = 30 °; ∟BAD = ∟BCD = 30 ° (ΔABC - равнобедренный).
Рассмотрим ΔАКС (∟К = 90 °, АК - высота):
АК - катет, лежащий напротив угла 30 °, тогда АК = 1 / 2АС; АК = 18: 2 = 9 (см).
ответ: Высота AK= 9 см
Відповідь:
Пояснення: