

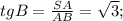 Угол В равен 60 градусов.
Угол В равен 60 градусов.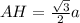
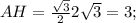 как высота правильного треугольника АВС.
как высота правильного треугольника АВС.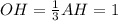 O лежит на пересечении медиан( высот, биссектрис) и делит АН в отношении 2:1, считая от А.Изпрямоугольного треугольникаSOH находим SO:
O лежит на пересечении медиан( высот, биссектрис) и делит АН в отношении 2:1, считая от А.Изпрямоугольного треугольникаSOH находим SO: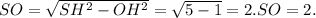
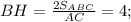 Из треугольника SBH по теореме Пифагора найдём SH:
Из треугольника SBH по теореме Пифагора найдём SH: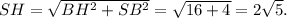
Чертёж смотрите во вложении.
Пусть АВ - длина высоты фабричной трубы, ВС - длина высоты тени от фабричной трубы, DE - длина высоты столба, а ЕС - длина высоты тени от столба. Пусть АВ = х.По условию - ВС = 35 м.DE = 7 м.ЕС = 5 м.Рассмотрим прямоугольные ΔАВС и ΔDEC. У них есть общий острый ∠С, поэтому, ΔАВС ~ ΔDEC (по первому признаку подобия прямоугольных треугольников).
В подобных треугольниках против равных углов лежат сходственные стороны.
То есть, DE и АВ - сходственные стороны.
Составим пропорцию и решим её-
АВ = х = 49 м.
ответ: 49 м.