Четырёхугольник можно вписать в окружность в том случае, если сумма противолежащих углов четырёхугольника равна 180 градусов. По условию четырёхугольник вписан в окружность. Значит и сумма противоположных углов равна 180. Отсюда имеем:
115 + х = 180 , > х = 180 - 115 = 65 градусов.
63 + х = 180, > х = 180 - 63 = 117 градусов.
Следовательно, градусные меры остальных углов 4-угольника соответственно равны 65 и 117 градусов. Кроме того, в сумме градусные меры 4 углов 4-угольника дают 360 градусов, что говорит об истинности решения.
ответ: 65 и 117
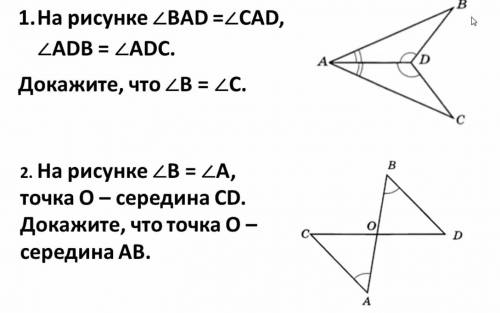
1. Рассмотрим треугольник АВD и треуг. ADC, в них: угол вад= углу сад(по усл.), угол адб=углу адс(по усл), AD-общая. Из этого следует, что треуг ABD=треуг ADC( ПО СТОРОНЕ И ДВУМ ПРИЛЕЖАЩИМ К НЕЙ УГЛАМ)
2 рассмотрим треуг BOD и треуг COA, в них: угол А= углу В, СО=ОD(по усл.), угол СОА= углу ВОD( как вертикальные). Из этого следует, что треуг ВОD= треуг COA. (по стороне и 2 углам)
СО=ОD(как соответственные элементы в равных фигурах)