2√153 см ≈ 24,74 см
Объяснение:
1) 24 - це довжина гіпотенузи; а тому кут, який вона утворює з прямою дорівнює 45°, то обидва катета (один з них - довжина проекції, а інший-висота, відстань від точки до прямої) рівні. Приймемо довжину катета за х.
Тоді, згідно з теоремою Піфагора:
х² + х² = 24²
2х²=576
х² = 288
х = √288 см
2) Довжину другої похилої L знаходимо також за теоремою Піфагора:
L = √(18² + (√288)²) = √(324 + 288) = √612 = 2√153 ≈ 24,74 см
Відповідь: 2√153 см ≈ 24,74 см
1) 24 - это длина гипотенузы, а т.к. угол, который она образует с прямой равен 45°, то оба катета (один из них - длина проекции, а другой - высота, расстояние от точки до прямой) равны. Примем длину катета за х.
Тогда, согласно теореме Пифагора:
х² + х² = 24²
2х²=576
х² = 288
х = √288 см
2) Длину второй наклонной L находим также по теореме Пифагора:
L = √(18² + (√288)²) = √(324 + 288) = √612 = 2√153 ≈ 24,74 см
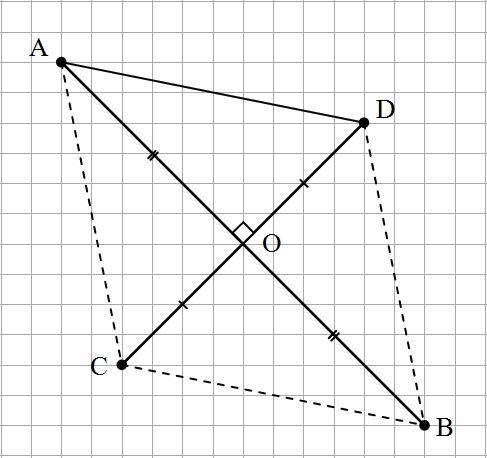
1). См. рис.1
По условию, т.О - середина отрезков АВ и СD.
Кроме того, AB⊥CD.
Четырехугольник, в котором диагонали пересекаются под прямым углом и делятся точкой пересечения пополам, является ромбом.
Следовательно, AD = DB = BC = CA = 17 (см)
В ΔАОD и ΔСОB:
АО = ОВ; СО = ОD; ∠АОD = ∠COB = 90°
Следовательно, прямоугольные треугольники ΔАОD и ΔСОB равны по двум катетам.
---------------------------------
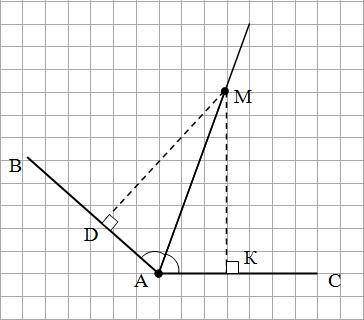
2). См. рис.2
В ΔADM и ΔАКМ:
∠ADM = ∠AKM = 90°
∠DAM = ∠KAM = 70° (АМ - биссектриса ∠ВАС)
Тогда:
∠DMA = ∠KMA = 180 - (90 + 70) = 20°
Следовательно, прямоугольные треугольники ΔADM и ΔАКМ равны по общей гипотенузе и острому углу.
--------------------------------
3). В ΔАВЕ и ΔDCE:
∠ABE = ∠DCE = 90°
∠BEA = ∠CED, как вертикальные
Тогда:
∠ВАЕ = ∠СDE = 20°
и ∠BEA = ∠CED = 180 - (90 + 20) = 70°
Так как ∠ВАЕ = ∠СDE = 20° и АВ = СD, то:
ΔABE = ΔDCE по катету и прилежащему острому углу.
Величина угла ∠АЕD:
∠АЕD = 180 - 70 = 110°
В ΔАЕD:
AE = ED, как гипотенузы в равных треугольниках.
Следовательно, ΔАЕD - равнобедренный и:
∠EAD = ∠EDA = (180 - 110) : 2 = 35°
В ΔABD и ΔACD:
∠BAD = ∠CDA = 20 + 35 = 55°
и АВ = CD
Тогда:
ΔABD = ΔACD по катету и прилежащему острому углу.
2х
СОСТАВИМ УРАВНЕНИЕ
2Х+2Х+Х=16,5
5Х=16,5
Х=16,5:5
Х=3,3 ( ОСНОВАНИЕ)
3,3*2=6,6 ( БОКОВАЯ СТОРОНА)