Из трёх задач только №617 имеет решение.
В задаче №618 угол между высотой и биссектрисой составляет 90 градусов, то есть невозможно построить третью точку.
В задаче №619 взаимное расположение заданной точки В, высоты и биссектрисы из разных вершин не даёт решения.
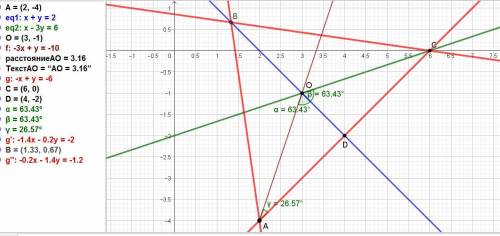
№617) Дана вершина А(2; -4) и уравнения биссектрис двух его углов х + у - 2 = 0 и х - 3у - 6 =0.
Находим точку пересечения биссектрис, решая систему:
{х + у - 2 = 0.
{х - 3у - 6 = 0. Вычитаем:
4у + 4 = 0, у = -4/4 = -1, х = 2 - у = 2 - (-1) = 3. Точка О(3; -1).
Через эту точку и вершину А(2; -4) проводим ещё одну биссектрису.
Вектор АО = (1; 3). Уравнение АО: (х - 2)/1 = (у + 4)/3 или в общем виде
3х - у - 10 = 0. Угловой коэффициент равен к(АО) = 3.
Из уравнений биссектрис находим их угловые коэффициенты:
к(ОД) = -1, к(ОС) = 1/3.
Находим тангенсы углов АОД и ДОС по их угловым коэффициентам.
к(АОД) = (3 - (-1))/(1 + 3*(-1)) = 4/-2 = -2.
к(ДОС) = (-1 - (1/3))/(1 + (-1)*(1/3)) = -4/2 = -2.
Как видим они равны, значит, биссектриса ОД является и высотой, а сторона АС перпендикулярна биссектрисе ОД.
Уравнение стороны АС определяем из уравнения ОД по свойству - коэффициенты при х и у меняются, один из них с другим знаком.
АС: -х + у + С = 0.Для определения слагаемого С подставим координаты точки А. -2 - 4 + С = 0. Отсюда С = 6.
Находим уравнение первой стороны:
АС: -х + у + 6 = 0 или х - у - 6 = 0.
Далее, используя значение угла между стороной и биссектрисой, находим угловые коэффициенты двух других сторон.
к(ОАС) = (3-1)/(1 + 3*1) = 2/4 = 1/2.
к(АВ) = (3 + (1/2))/91 + (1/3)*(1/2)) = -7.
Уравнение АВ: у = -7х + С. Подставляем координаты точки А.
-4 = -7*2 + С, отсюда С = -4 + 14 = 10.
Уравнение АВ: у = -7х + 10 или 7х + у - 10 = 0.
Координаты точки С находим, решая систему уравнений биссектрисы ОС и найденной стороны АС. с(
4 0).Аналогично находим уравнение ВС: к(ВС) = -1/7.
ВС: у = у = (-1/7)х + С. Точку С: 0 = (-1/7)*6 + С, отсюда С = (6/7)
Уравнение ВС: у = (-1/7)х + (6/7) или х - 7у - 6 = 0.
а) 2√3 б) 6.
Объяснение:
Условие задачи.
Сторона AB, равная 8, правильного треугольника ABC лежит в плоскости альфа, а длины проекций двух других его сторон на эту плоскость равны 2√7. Найдите: а) длину проекций медианы CK данного треугольника на плоскость альфа; б) расстояние от точки C до плоскости альфа
Решение.
1) Так как ΔАВС - правильный, то АВ = ВС = АС = 8.
2) В правильном треугольнике АВС его медиана СК является высотой, соответственно и в проекции АВС₁ треугольника АВС на плоскость α проекция С₁K медианы СК является и медианой, и высотой равнобедренного ΔАВС₁ со сторонами: АВ = 8, ВС₁ = АС₁ = 2√7.
3) В прямоугольном ΔАКС₁ сторона АС₁ является гипотенузой, а стороны АК и КС₁ являются катетами, при этом АК = АВ/2 = 8/2 = 4.
По теореме Пифагора находим длину проекции медианы:
С₁K = √ ((АС₁)²-(АК)²) = √ ((2√7)²-(4)²) = √ (4*7 - 16) = √12 = 2√3
Таким образом, длина проекции медианы CK данного треугольника на плоскость α = 2√3
4) В прямоугольном ΔАСС₁, образованном стороной АС треугольника АВС, её проекцией АС₁ на плоскость α, а также перпендикуляром СС₁, опущенным из точки С на плоскость α и являющимся кратчайшим расстоянием от точки С до плоскости α, сторона АС является гипотенузой треугольника АСС₁, а стороны АС₁ и СС₁ - его катетами. ПО теореме Пифагора находим СС₁:
СС₁ = √ ((АС)²-(АС₁)²) = √ ((8)²-(2√7)²) = √ (64 - 4*7) = √36 = 6.
Таким образом, расстояние от точки C до плоскости альфа равно 6.
ответ: а) длина проекции медианы CK данного треугольника на плоскость альфа равна 2√3; б) расстояние от точки C до плоскости альфа равно 6.
1) центр
2) диаметр
3) хорда