Відповідь:
катети: 3 см, 3√3 см; кути: 90°, 30°
Пояснення: Описка у завданні: кут вимірюється у градусах, а не см
1.Сума кутів будь-якого трикутника дорівнює 180°,
Оскільки трикутник прямокутний, один із кутів дорівнює 90°, а іншій:
180-(90+30)=60°
2.У прямокутному трикутнику катет, який лежить напроти кута у 30°, дорівнює 1/2 гіпотенузи, тому один з катетів: 6:2=3 см
3.За теоремою Піфагора квадрат гіпотенузи дорівнює сумі квадратів катетів ⇒другий невідомий катет дорівнює: 6²-3²=36-9=27, √27=√9*3=3√3 (см)
Треугольники А0Д и В0С - подобные (уг.В0С = уг.А0Д как вертикальные; уг.СВ0 = уг.АД0 как внутренние накрест лежащие при параллельных прямых АД и ВС и секущей ВД).
Площадь тр-ка ВОС равна S1 = 0,5ВС·Н1
Площадь тр-ка АОД равна S2 = 0,5АД·Н2
При этом Н1:Н2 = к -коэфиициент подобия, а S1 : S2 = к²
S1 : S2 = 0,5ВС·Н1 : 0,5АД·Н2
к² = к· ВС: АД
к = 9/16
Итак, нашли коэффициент подобия.
Из подобия тех же тр-ков следует, что ОВ:ОД = 9/16, но ОД = АС - ОВ и
ОВ: (АС - ОВ) = 9/16
16·ОВ = 9·(АС - ОВ)
16·ОВ = 9·АС - 9·ОВ
25·ОВ = 9·АС
ОВ = 9·АС/25 = 9·18:25 = 6,48
ответ: ОВ = 6,48см
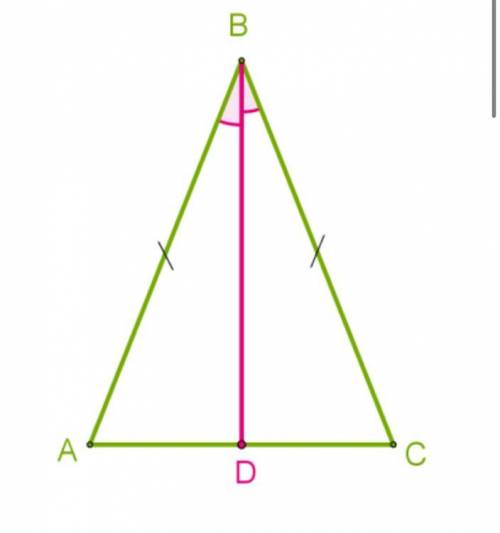
Рассмотрим треугольники ΔABD и ΔBCD.
1. так как прилежащие к основанию углы данного равнобедренного треугольника равны, то ∡A = ∡C ;
2. так как проведена биссектриса, то ∡ABD = ∡CBD ;
3. AB = BC , так как данный ΔABC — равнобедренный.
По второму признаку равенства треугольников ΔABD и ΔBCD равны.
Значит, равны все соответствующие элементы, в том числе стороны AD = CD. А это означает, что отрезок является медианой данного треугольника и делит сторону пополам.