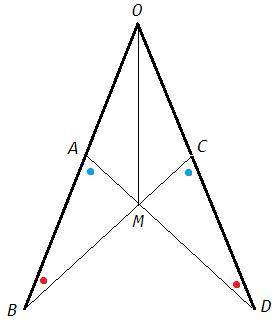
OB =OA+AB =OC+CD =OD
△BOC=△DOA (по двум сторонам и углу между ними), ∠B=∠D
∠AMB=∠CMD (вертикальные)
В треугольниках BAM и DCM два угла равны, следовательно все углы равны, ∠BAM=∠DCM
△BAM=△DCM (по стороне и прилежащим к ней углам), AM=CM
△AOM=△COM (по трем сторонам), ∠AOM=∠COM, OM - биссектриса ∠AOC.
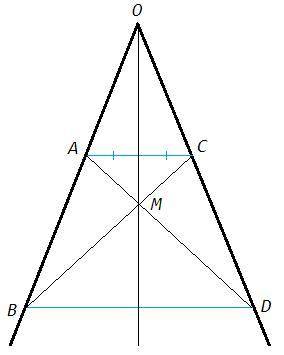
Или
Прямые AC и BD отсекают на сторонах угла равные отрезки, следовательно прямые параллельны (теорема Фалеса), ACDB - трапеция. По теореме о четырех точках трапеции OM проходит через середину AC и является в равнобедренном треугольнике AOC медианой и биссектрисой.
Пусть АВ - исходное положение "журавля", СЕ - после подъема короткого плеча.
Рассмотрим треугольники АСК и ВЕК:
АК : КВ = 1 : 4,
СК : КЕ = 1 : 4,
углы при вершине К равны как вертикальные, значит
ΔАСК подобен ΔВЕК по двум пропорциональным сторонам и углу между ними. Тогда
СА : ВЕ = 1 : 4
ВЕ = 4 · СА = 4 · 0,5 = 2 м
ответ: конец длинного плеча опустится на 2 м