Дан цилиндр, в котором проведено сечение. Это сечение пересекает основание по хорде, стягивающей дугу, градусная мера которой равна β. Диагональ сечения образует с плоскостью основания угол α. Найдите площадь сечения, если радиус основания цилиндра равен R.
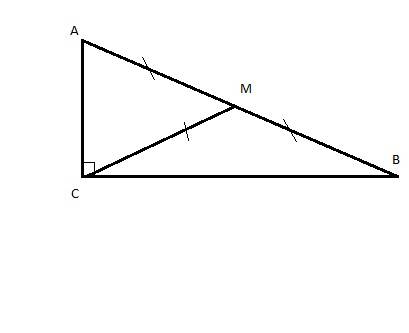
пусть коэффициент отношения - х, тогда х+2х=90 градусов, 3х=90, х=30 градусов. 90-30=60 градусов. Прямой угол разделился медианой на углы в 30 и 60 градусов. Медиана, проведённая из прямого угла, = половине гипотенузы, поэтому
СК=АК= КВ=10. Треугольник АКС - равнобедренный с углом 60 градусов, значит, он равносторонний и АС=10, угол СКВ= 180-60=120 градусов т. к. углы СКВ и СМА - смежные. Катет ВС лежит против угла в 120 градусов, следовательно, он больше катета АС, т. к. против большего угла лежит большая сторона. ответ 10