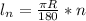, где n - градусная мера соответственного центрального угла.
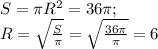, где S - площадь круга.
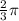см.
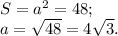
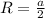, где a - сторона квадрата.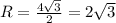
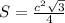, где c - сторона правильного треугольника.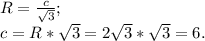
.
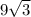см.
* * * * * * * * * * * * * * * * * * * * * * *
Найдите боковую сторону AB трапеции ABCD, если ∠ABC =60° , ∠BCD =135°, а CD = 27.
ответ: 9√6.
Объяснение: Через вершину B проведем прямую параллельную
боковой стороне СD до пересечения с основанием AD в точке E .
BCDE → параллелограмм ⇒ BE =CD =27 ; ∠CBE =180°-∠BCD =135° .
Из ΔBAE : AB/sin(∠BEA) = BE/sin(∠BEA) * * *теорема синусов * * *
AB=BE*sin(∠BEA)/sin(∠BEA)=27sin45°/sin(180°- 60°) = 27*sin45°/sin60° =
= 9√6. * * * sin45°= (√2)/2 , sin60°=(√3)/2 * * *
E - середина AB
Противоположные стороны параллелограмма параллельны и равны.
AB=CD => AB/2=CD/2 => AE=CM
AECM - параллелограмм (AE||CM, AE=CM)
=> CE||AM
BH⊥AM => BH⊥CE
BE=EA => BF=FH (т Фалеса)
CF - высота и медиана в △BCH => △BCH - р/б
CH=BC=b