4,85 ед.
Объяснение:
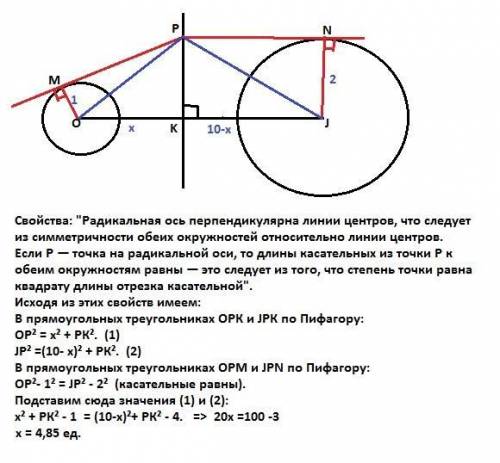
Свойства: "Радикальная ось перпендикулярна линии центров, что следует из симметричности обеих окружностей относительно линии центров.
Если P — точка на радикальной оси, то длины касательных из точки P к обеим окружностям равны — это следует из того, что степень точки равна квадрату длины отрезка касательной".
Исходя из этих свойств имеем:
В прямоугольных треугольниках ОРК и JРК по Пифагору:
ОР² = х² + РК². (1)
JР² =(10- х)² + РК². (2)
В прямоугольных треугольниках ОРМ и JPN по Пифагору:
ОР²- 1² = JP² - 2² (касательные равны).
Подставим сюда значения (1) и (2):
х² + РК² - 1 = (10-х)²+ РК² - 4. => 20x =100-3.
х = 4,85 ед.
8 см
Объяснение:
Пусть дан треугольник АВС. АС=30см. Обозначим точки касания вписанной окружности и сторон треугольника АС, АВ и ВС соответственно К, Т, Р.
Тогда по условию задачи ВТ=12 см и АТ=14 см
Тогда АТ=АК= 14 см
КС= АС-АК=30-14=16 см
КС=РС=16 см
ВР=ВТ=12 см
Тогда АВ=АТ+ВТ=12+14=26 см, ВС =ВР+РС=12+16=28 см
Тогда периметр Р= 26+28+30=84 см
Тогда полупериметр р=Р:2=84:2=42
Тогда площадь треугольника по теореме Герона
S=sqrt(p*(p-a)*(p-b)*(p-c))= sqrt(42*12*14*16)=336
С другой стороны площадь треугольника может быть вычислена по формуле S=p*r=42*r=336
=> r=336/42
r=8