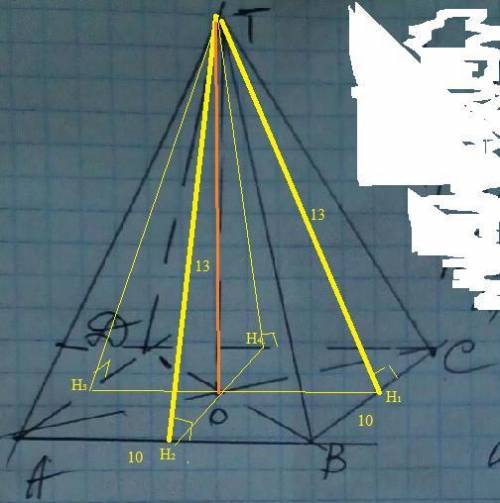
Расстояние от точки до сторон квадрата равно 13 см. Найдите расстояние от точки до плоскости квадрата, если сторона квадрата равна 10 см. можете объяснить, с рисунком
Объяснение:
Расстояние от точки Т до плоскости отрезок ТО ⊥ ( АВС) . Значит ТО перпендикулярен любой прямой лежащей в плоскости.
Т.к. расстояние -это перпендикуляр, то опустим перпендикуляры из точки Т на стороны квадрата : ТН₁ , ТН₂ , ТН₃ , ТН₄. Тогда прямоугольные треугольники ( на рисунке желтые) равны по катету и гипотенузе ( апофема боковой грани).⇒точка О -центр вписанной окружности и еще т. пересечения диагоналей квадрата.
Н₁ Н₃= 10 , ОН₁=5 , из ΔТОН₁ , по т. Пифагора ТО=√(13³-5²)=√144=12 (см)
треуг ABC- равнобедренный
РтреугАВС=15,6
АВ=ВС(свойство равнобедр. треуг)
АВ и ВС - х
АС - х+3
Найти: АВ,ВС,АС
Решение:
РтреугАВС= АВ+ВС+АС
РтреугАВС=х+х+х+3=15,6м
1)х^3+3=15,6
х^3=15,6-3
х^3=12,6
х=12,6:3
х=4,2(м) - АВ и ВС