∠ABC = 67°
Объяснение:
Дано: ΔABC - прямоугольный
∠C=90°
СО - биссектриса
CH - высота
∠OCH = 22°
Найти: бОльший угол ΔABC
Т.к. биссектриса делит угол пополам, а она проведена из прямого угла,следовательно ∠ACO=∠OCB=90°:2=45°
Угол ∠OCB состоит из углов ∠OCH и ∠HCB. Из этого мы делаем вывод,что ∠HCB=∠OCB-∠OCH = 45°-22°=23°
ΔСНВ - прямоугольный,т.к. CH - высота. Из этого ∠ABC=90°-∠HCB=90°-23°=67°
ΔСНВ - прямоугольный(по условию).Из этого ∠ВАC=90°-∠ABC=90°-67°=23°
Мы видим, что ∠ABC > ∠ВАC => в ответ пишем градусную меру угла ∠ABC

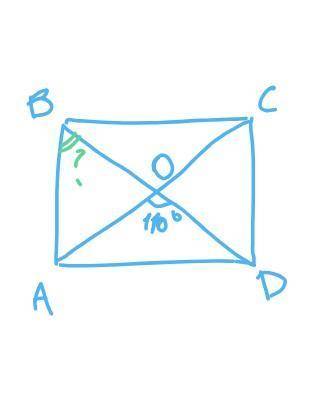
Диагонали прямоугольника имеют одинаковую длину, AC = BD;
Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам,
AO = OC = BO = OD;
Получается, треугольник ABO — равнобедренный (BO = AO), углы при основании равнобедренного треугольника равны, ∠ABO = ∠OAB;
∠ABD — это тот же ∠ABO;
∠AOB + ∠AOD = 180° (лежат на одном развёрнутом угле BOD), ∠AOB = 180° – ∠AOD = 180° – 110° = 70°;
Сумма углов треугольника равна 180°,
∠ABO + ∠AOB + ∠OAB = 180°,
Подставляем, что ∠ABO = ∠OAB, получаем
2 × ∠ABO + ∠AOB = 180°,
2 × ∠ABO = 180° – ∠AOB = 180° – 70° = 110°,
∠ABO = 110° ÷ 2 = 55° = ∠OAB
ответ: 55°
Объяснение:
отрезок ЕD = 14 дм и составляет 5 частей, отрезок ML составляет 12 частей, тогда
14дм - 5 частей
х дм - 12 частей
х= 14 * 12 : 5
х= 33,6 дм длина отрезка ML