
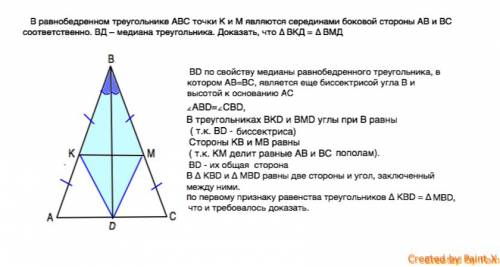
В равнобедренном треугольнике АВС точки К и М являются серединами боковой стороны АВ и ВС соответственно. ВД – медиана треугольника. Доказать, что ∆ ВКД = ∆ ВМД
ВД по свойству медианы равнобедренного треугольника, в котором АВ=ВС, является еще биссектрисой угла В и высотой к основанию АС
∠АВД=∠СВД,
В треугольниках ВКД и ВМД углы при В равны ( ВД - биссектриса угла АВС)
Стороны КВ и МВ равны ( т.к. КМ делит равные АВ и ВС пополам).
ВД - их общая сторона
В ∆ КВД и ∆ МВД равны две стороны и угол, заключенный между ними.
По первому признаку равенства треугольников ∆ КВД = ∆ МВД, что и требовалось доказать.
36ед
Объяснение:
Медианы точкой пересечения делятся в отношении 2:1 начиная от вершины треугольника.
ВО:ОК=2:1
ВК=3*ОК=3*2=6ед
ВК- высота, медиана и биссектрисса равнобедренного треугольника ∆АВС;
АК=КС
АК=АС/2=16/2=8ед.
∆АВК- прямоугольный треугольник
По теореме Пифагора
АВ=√(ВК²+АК²)=√(8²+6²)=√(64+36)=√100=
=10ед.
АВ=ВС, по условию
Р(∆АВС)=АВ+ВС+АС=10+10+16=36ед