Если в равнобедренной трапеции провести высоты ВН и СК, то получим НВСК - прямоугольник (ВС║КН, так как основания трапеции параллельны, ВН║СК как перпендикуляры к одной прямой), тогда
ВС = КН и ВН = СК.
ΔАВН = ΔDCK по гипотенузе и катету (АВ = CD, так как трапеция равнобедренная, ВН = СК), тогда
АН = DK = (AD - KH)/2 = (AD - BC)/2.
Площадь трапеции:
Sabcd = (AD + BC)/2 · BH
Воспользуемся этими выводами для решения задач:
а) AH = DK = (17 - 11)/2 = 3 см
ΔАВН прямоугольный с гипотенузой, равной 5 см и катетом 3 см, значит он египетский и
ВН = 4 см.
Sabcd = (17 + 11)/2 · 4 = 28/2 · 4 = 14 · 4 = 56 см²
б) AH = DK = (8 - 2)/2 = 3 см
ΔABH: ∠AHB = 90°, ∠BAH = 60°, ⇒ ∠ABH = 30°.
AB = 2AH = 6 см по свойству катета, лежащего напротив угла в 30°,
по теореме Пифагора:
BH = √(AB² - AH²) = √(36 - 9) = √27 = 3√3 см
Sabcd = (8 + 2)/2 · 3√3 = 15√3 см²
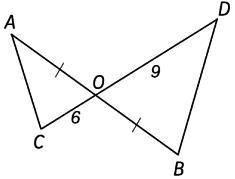
S(∆AOC)/S(∆DOB)=2/3
Объяснение:
Пусть АО будет х, тогда ВО тоже будет х.
∠АОС=∠DOB, вертикальные углы,
Углы обозначим α (альфа)
S(∆AOC)=1/2*AO*OC*sin<AOC=
=1/2*CO*x*sinα
S(∆DOB)=1/2*DO*OB*sin<DOB=
=1/2*DO*x*sinα.
S(∆AOC)/S(∆DOB)=(½*CO*x*sinα)/(½*DO*x*sinα) (сократили что можно и получили)
S(∆AOC)/S(∆DOB)=CO/DO=6/9=2/3