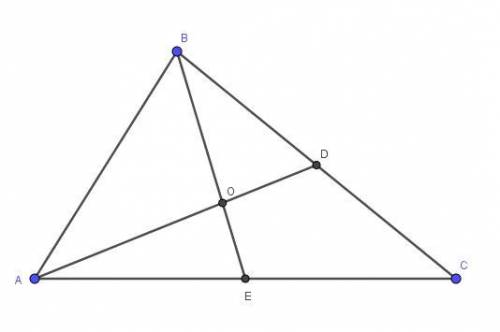
В треугольнике АВС известны длины сторон АВ =8 и АС = 64.
Точка О центр окружности, описанной около треугольника АВС. Прямая ВD перпендикулярная прямой АО , пересекает сторону АС в точке D. Найдите СD.
–––––––––––––––––
Продлим ВD до пересечения с окружностью в точке М.
Хорда МВ перпендикулярна радиусу ОА ( по условию) и при пересечении с ним делится пополам ( свойство).
Тогда радиус ОА делит угол ВОМ пополам. Дуги АМ и АВ, на которые опираются равные центральные углы МОА и ВОА, также равны.
Отсюда следует равенство углов АВМ и ВСА - опираются на равные дуги.
В треугольниках АВС и АВD угол ВАС общий, ∠АВD=∠ВСА ⇒
∆ АВС ~ ∆ АВD по 1-му признаку подобия. Из подобия следует отношение:
АВ:АС=АD:АВ
АВ²=АD•AC
64=AD•64⇒ AD=1
CD=64-1=63 (ед. длины)
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника.
Пусть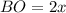 
см и 
см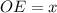, тогда 
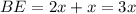, что по условию он равен 9 см.
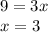
Следовательно,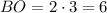 
см и 
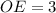см
Аналогично, пусть теперь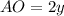 
см и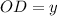 
, тогда 
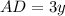и по условию равен 12 см
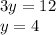
Таким образом,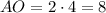 
см и 
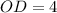см.
По условию медианы треугольника AD и BE взаимно перпендикулярны, следовательно
По теореме Пифагора из прямоугольного треугольника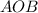 
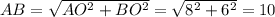см
По теореме Пифагора из прямоугольного треугольника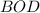 
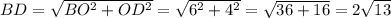см
Тогда 
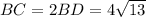см
Из прямоугольного треугольника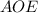 
по теореме Пифагора
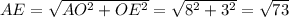см
Тогда 
см
ответ: 
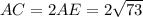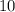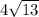см;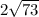 
см; 
см.
™ Zmeura1204
Объяснение:
1)
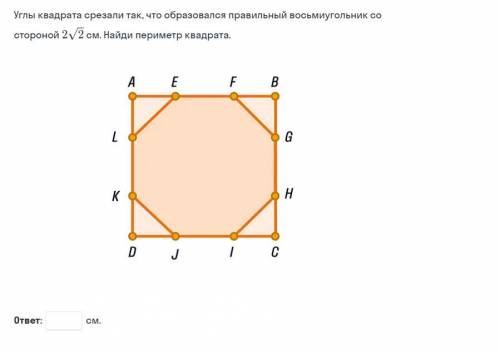
∆LAE=∆FBG=∆HCI=∆JDK
∆LAE- равнобедренный прямоугольный треугольник
АЕ=LE/√2=2√2/√2=2см.
АВ=2*АЕ+ЕF=2*2+2√2=4+2√2 см.
Р(ABCD)=4*AB=4(4+2√2)=16+8√2 см
ответ: Р(ABCD)=16+8√2см.
2)
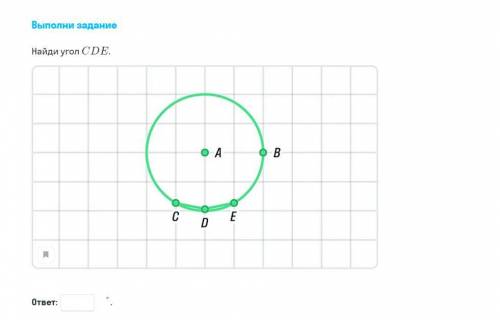
В окружность вписанный двенадцатиугольник.
Формула нахождения градусной меры угла.
180°(n-2)/n, где n=12 количество углов.
180°(12-2)/12=1800/12=150°
ответ: ∠СDE=150°
3)
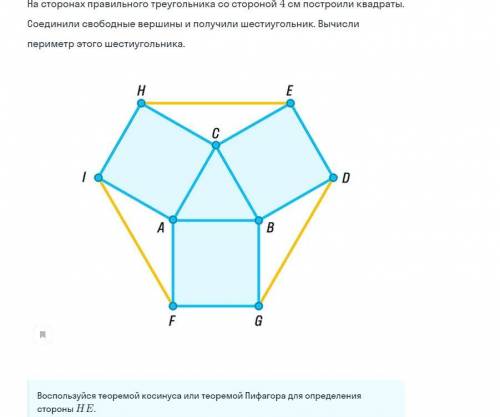
В равностороннем треугольнике все углы по 60°
∠АСВ=60°
В квадрате все углы по 90°
∠ЕСВ=90°; ∠НСА=90°
Полный угол равен 360°
∠НСЕ=360°-∠ЕСВ-∠НСА-∠АСВ=
=360°-90°-60°-90°=120°
∆НСЕ- равнобедренный треугольник
НС=СЕ, стороны квадрата.
Сумма углов в треугольнике равна 180°
В равнобедренном треугольнике углы при основании равны
∠НЕС=(180°-∠НСЕ)/2=(180°-120°)/2=30°
СМ- высота, медиана и биссектрисса равнобедренного треугольника ∆НСЕ
∆СМЕ- прямоугольный треугольник.
cos∠MEC=ME/CE
cos30°=√3/2
√3/2=ME/4
ME=4√3/2=2√3см
НЕ=2*МЕ=2*2√3=4√3 см.
Рз.ф.=3*ЕD+3*HE=3*4+3*4√3 =12+12√3см
ответ: 12+12√3см
Обозначение:
Рз.ф.-периметр заданной фигуры.