Объяснение:
Задача 1:
Так как сумма углов прилежащих к одной стороне равна 180 градусов, значит углы данные в задаче- противолежащие. Противолежащие углы у параллелограмма равны, следовательно:
A + C= 62 равно 2A=62
Пусть A=x, тогда
2x=62
x=31 градус = угол А и следовательно=уголу C (противолежащие углы парал. равны)
Сумма прилежащих к одной стороне углов равна 180 градусов, следовательно, угол B= 180-A=180-31=149 градусов
ответ: угол B=149 градусов
Задача 2:
Так как противолежащие углы параллелограмма равны, а сумма углов прилежащих к одной стороне равна 180, то можно составить уравнение
Пусть угол A - x. Тогда угол D=x+70
x+(x+70)=180
2x+70=180
2x=110
x= 55- градусов угол A
1) D=180 - A= 180-55=125 градусов
ответ: 125 градусов = угол D
В треугольнике две стороны равны 10 см и 17 см, а высота, опущенная на третью, равна 8 см. найти наименьшую из площадей возможных треугольников
Объяснение:
S(треуг)= 1/2*а*h. Пусть АВ=17 см,ВС=10 см, ВН=8 см, ВН ⊥АС.
Возможные треугольники с высотой равной 8 см это ΔАВС, ΔАВН, ΔВСН. У всех перечисленных треугольников одинаковая высота, значит чем меньше основание , тем меньше площадь треугольника.
АС >АН и АС>СН, тк АС это сумма АН и СН.
Т.к ВН-высота, то АВ и ВС наклонные . А чем больше длина наклонной , тем больше проекция : АВ>BC⇒АН>СН.
Значит СН<AH<AC.
ΔCВН-прямоугольный , по т. Пифагора НС=√(10²-8²)=6 (см)
S(ΔCBH)=1/2*6*8=48 (см²)
Объяснение:
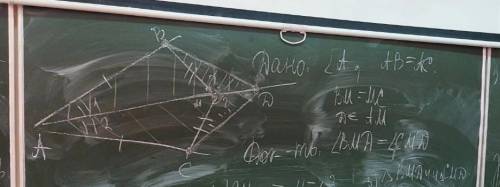
Рассмотрим треугольники △ABM и △АСМ. У них АВ=АС, ВМ=СМ по условию, а АМ - общая. => △ABM=△АСМ по 3му признаку.
=> <BMA=<CMA.
А значит равны и смежные с ними углы <BMD=<CMD. Чтд.