Задание 1.
Возьмем точку А , К и Р, они образуют какую то плоскость (по определению: любые три точки не лежащие на одной прямой образуют плоскость),
2) так как К Р Т лежат на одной прямой , то Т так же лежит в плоскости ( по определению : если две точки прямой лежат в плоскости то все точки прямой лежат в этой плоскости) - следовательно раз К и Р лежат в одной плоскоси с А, то и Т так же будет лежать в одной плоскости с А.
Задание 2.
Аксиомы стереометрии. 1) через 3 точки, не лежащие на одной прямой, можно провести плоскость, и только одну. Проводим через А и любые две из оставшихся, например, M и N. Точка Р также лежит в этой плоскости, т.к 2) если две точки прямой лежат в плоскости, то вся прямая лежит в этой плоскости. Известное следствие из аксиом: через прямую и точку, не лежащую на ней всегда можно провести плоскость, и притом только одну.
Задание 3.
Через две прямые пересекающиеся в одной точке можно провести только одну плоскость. И если другие прямые пересекаются с вышеназванными прямыми, то они тоже находятся в одной с ними плоскости. А вот через точку можно провести любое колическво прямых и многие из них будут находиться в других плоскостях.
10. Площа трикутника дорівнює добутку радіусу r вписаного кола і полупериметра р.
r=(a+b-c):2 , де а та b - катети, c -гіпотенуза.
a+b=P-с=60-c
r=(60-c-c):2=30-c
Також r=S:p; тоді
S=h*c:2
S=12*c:2=6c
р=60:2=30
r=6c/30=c/5
Отже
c/5=30-c
150-5c=c
6c=150
c=25 см
r=25/5=5 см
S=r*p=5*30=150 см².
Відповідь: 150 см²
12. Нехай дано трикутник АВС - прямокутний, ∠ А - 90°, ВС - гіпотенуза. ВС=32+18=50 см.
АН - висота.
Площа трикутника дорівнює 1\2 * ВС * АН.
АН=√(ВН*СН)=√(32*18)=√576=24 см.
S = 1\2 * 50 * 24 = 600 cм²
Відповідь: 600 см²
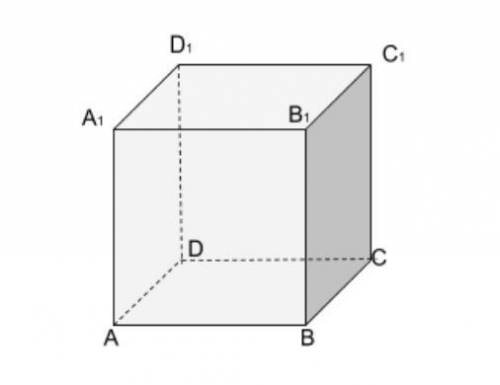
Пусть дана плоскость ACD1 в виде линий пересечения её с гранями куба.
Действия:
1) Проводим диагональ DB основания.
Этим самым мы находим точку О, через которую проходит плоскость, перпендикулярная к заданной.
2) Проводим прямую D1O.
Эта прямая - линия пересечения заданной плоскости и плоскости, перпендикулярной к ней.
3) Проводим отрезок ВЕ, перпендикулярный к D1O.
Задание выполнено.
Желающие могут определить фактическую длину такого перпендикуляра по заданным размерам куба.
Примем длину ребра куба, равную а, длину перпендикуляра - х.
Половина диагонали основания равна а√2/2.
Длина отрезка D1O равна:
D1O = √(а² + (а√2/2)²) = √(а² + 2а²/4) = √(6а²/4) = а√3/√2.
Из подобия треугольников составляем пропорцию.
x/(а√2/2) = a/а√3/√2.
Отсюда х = а√3/3.