Відповідь:
Пояснення:

угол ABC=альфа
угол KCS=угол KAS=угол KBS=бэта
G-основание высоты KG, проведенной к СS
Тогда KG=М
Основание высоты - центр описанной окружности(середина гипотенузы)Радиус описаной окружности равен R=KG\sin (KCG)=
M\sin(KCS)=M\(sin бэта)
Высота пирамиды равна R*tg (KCG)=M\(sin бэта)*tg бєта=
=M*cos бэта
Гипотенуза равна =2*радиус описанной окружности
Гипотенуза AB=2*m\(sin бэта)
Катет BC=AB*cos (ABC)=2*M\(sin бэта)*cos альфа
Катет AC=AB*sin (ABC)=2*M\(sin бэта)*sin альфа
Площадь прямоугольного треугольника равна половине произведения катетов
S=1\2*BC*AC=1\2*2*M\(sin бэта)*cos альфа*2*M\(sin бэта)*sin альфа=
M^2\(sin^2 бэта)*sin 2альфа
Обьем пирамиды 1\3*площадь основания(площадь равнобедренного треугольника)*высота
обьем пирамиды равен 1\3*M^2\(sin^2 бэта)*sin 2альфа*M*cos бэта=
M^3\3*sin 2альфа\(sin^2 бэта*cos бэта)
ответ:M^3\3*sin 2альфа\(sin^2 бэта*cos бэта)
p/s/ вроде так
1) треугольник АВС и треугольник А1В1С1 равны
значит ВА=В1А1и угол А=угол А1
Прямоугольные треугольники DВА и D1В1А1 равны за гипотенузой(ВА=В1А1) и острым углом(угол А=угол А1)
Из равности треугольников слдует равенство ВD = В1D1, то есть требуемое
2) Прямоугольные треугольники ADK и CEP равны за первым признаком равенства треугольников
угол K=угол Р=90 градусов АК=РС,DK=РЕ по условию.
Из равенства треугольников следует равенство углов
угол А=угол С, а за признаком равнобедрнного треугольника
треугольник АВС равнобедренный и АВ=ВС, что и требовалось доказать.
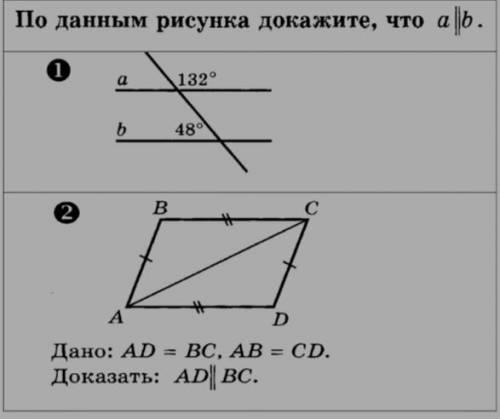
1)Угол 1 и угол в 132 градуса - вертикальные, следовательно угол 1 = 132 градуса ( так как вертикальные углы равны)
2)Угол 1 + угол в 48 градусов = 132 + 48 = 180 градусов
3)Так как угол 1 и угол в 48 градусов - односторонние и в сумме дают 180 градусов, следовательно а параллельно б
1)Рассматриваем два треугольника ABC и ACD. Они равны по третьему признаку (по трём сторонам) так как по условию AB=CD и AD=BC, а также AC у них общая сторона.
2)Так как треугольники равны, значит углы одного треугольника соответственно равны углам другого треугольника. Отсюда угол 1 = углу 2. Они накрест лежащие и равные, а значит прямые параллельны
Объяснение:
Выбранные углы 1 и 2 отмечены на фото