∠СED = 20°.
Объяснение:
Множество точек Е, удовлетворяющее условию нахождения точки D на серединном перпендикуляре к отрезку СЕ - это все точки окружности радиуса СD. Тогда все хорды этой окружности, исходящие из точки С, будут перпендикулярны радиусу этой окружности и делятся этим перпендикуляром пополам, то есть условие выполняется. Тогда максимальное расстояние ВЕ будет при расположении точки Е на пересечении прямой ВD и окружности, так как из всех секущих из точки В к окружности с центром в точке D максимальную длину имеет секущая, проходящая через центр этой окружности.
В равнобедренном треугольнике АВС ∠ВАС = (180-80):2 = 50°.
В прямоугольном треугольнике АВD ∠ВDА = 90-50 = 40° =>
Это внешний угол равнобедренного треугольника CDE, тогда, поскольку он равен сумме двух внутренних углов треугольника (∠DCE = ∠CED), не смежных с ним,
∠CED = 40:2 = 20°.
1) 150.
2) 15.
3) 18.
4) 270.
Объяснение:
Площадь трапеции определяется по формуле:
S=h(a+b)/2;
1) a=9+12=21; b=4; h=12.
S=12*(21+4)/2=6*25=150;
***
2) S=h(a+b)/2; a=3; b=9; h=? Высота (катет )лежит против угла в 30* и равна половине гипотенузы h=5/2=2.5;
S=2.5(3+9)/2;
S=2.5*12/2;
S=2.5*6=15.
***
3) Вероятно это равнобокая трапеция и углы при основаниях равны.
Проведем высоту из вершины тупого угла. Получим равнобедренный треугольник с углами по 45*, стороны которых (и высота) равны 9-2*3=9-6=3;
S=h(a+b)/2; h=3; a=3; b=9;
S=3(3+9)/2=3*12/2=18.
***
4) Все величины для нахождения площади известны.
S=h(a+b)/2; h=15; a=4; b=8+24=32;
S=15(4+32)/2;
S=15*36*2=15*18=270.
∠С=30°,∠А=90°,∠В=60°
Объяснение:
Дано: AD⊥BC, ВО=ОС. ∠ВАD=∠DАО=∠ОАС
Найти: ∠А,∠В,∠С ΔАВС
Пусть ∠ВАD=∠DАО=∠ОАС=х
1) Рассмотрим ΔВАО. АD - высота. ∠ВАD=∠DАО ⇒ АD - биссектриса.
Если в треугольнике медиана совпадает с биссектрисой, то треугольник равнобедренный. ⇒ΔВАО - равнобедренный. В равнобедренном треугольнике высота является также медианой. ⇒
ВD=DО=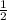
ВО= 
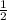ОС.
2) Дополнительное построение: Проведём ОМ⊥АС.
Рассмотрим прямоугольные треугольники АDО и АМО.
∠DАО=∠ОАС - по условию, АО - общая.
Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.⇒ΔАDО = ΔАМО
Из равенства треугольников следует равенство катетов:
DО = МО =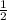
ВО= 
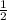ОС.
3) Рассмотрим прямоугольный треугольник ОМС (∠М=90°).
Из доказанного выше МО=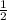
ОС. Т.е. катет МО равен половине гипотенузы ОС.
Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30°.Следовательно ∠С=30°
4) Рассмотрим прямоугольный треугольник АDC(∠D=90°).
По свойству острых углов прямоугольного треугольника
∠DАС=90°-∠С=90°-30°=60°.
По условию ∠DАС=2х ⇒ 2х=60°, х=30°
5) ∠ВАС=3х=3*30°=90°
∠А треугольника АВС = 90°
Так как сумма углов треугольника равна 180°, то ∠В треугольника АВС будет равен: ∠В=180°-∠А-∠С=180°-90°-30°=60°