формула нахождения высоты равностороннего треугольника:
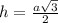
h-высота
а-сторона треугольника
тогда
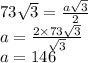
P∆=3a=3×146=438см
ответ: 438см
Дано:
MNP - треугольник
<M = 35
<N = 90
MN = 14 см
Найти:
PN = ?
MP = ?
< P = ?
Так, как в треугольнике сумма всех углов равна 180°, то>
<P = 180 - (<N+<M) = 180 - (35+90) = 180 - 125 = 55°
-------------------------------------------------------------------------------------
ЕСЛИ ВЫ НЕ ПРОХОДИТЕ СИНУСЫ В ДАННЫЙ МОМЕНТ, ТО ДАННОЕ РЕШЕНИЕ НЕ ДЛЯ ВАС!
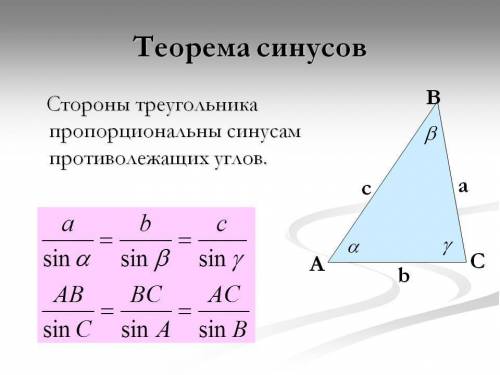
Данную задачу можно решить с теоремы синусов, которая утверждает, что стороны треугольника пропорциональны синусам противолежащих углов.
Значит:
MN/sin(<P) = NP/sin(<M) = MP/sin(<N) =>
14/sin(55) = NP/sin(35) , 14*sin(35)/sin(55) = NP
14/sin(55) = MP/sin(90), 14*sin(90) / sin(55) = MP = 14/sin(55)
PN = 14*sin(35)/sin(55)
MP = 14/sin(55)
<P = 55°
Вроде правильно....
438см
Объяснение:
Формула нахождения высоты равностороннего треугольника
h=a√3/2; где а-сторона треугольника.
а=2h/√3=2*73√3/√3=146см
Р=3а=3*146=438см