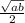, высота трапеции: h=2r=
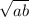=√8=2√2
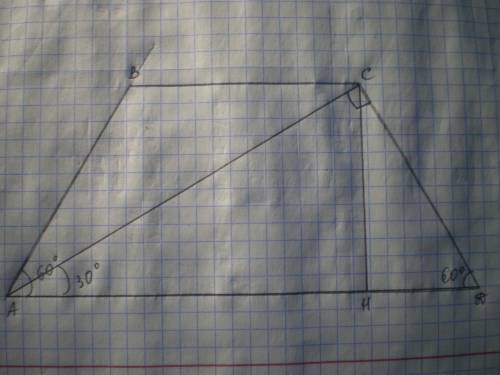
Дано: АВСД - трапеция, АВ=СД, АД=16√3, ∠А=∠Д=60°, АС⊥СД. Найти S(АВСД).
Решение: Проведем высоту СН, тогда S(АВСД)=(ВС+АД):2*СН.
Рассмотрим ΔАСД - прямоугольный, ∠Д=60°, тогда ∠САД=90-60=30°, а СД=1\2 АД=16√3:2=8√3.
Диагональ АС перпендикулярна к боковой стороне и делит угол А пополам, значит большее основание трапеции в два раза больше меньшего основания и её боковых сторон; и высота трапеции равна половине её диагонали.
СД=ВС=16√3:2=8√3;
АС²=(16√3)²-(8√3)²=768-192=576; АС=√576=24.
СН=1\2 АС=24:2=12.
S(АВСД)=(8√3+16√3):2*12=144√3 (ед²).
ответ: 144√3 ед²
65°
Объяснение:
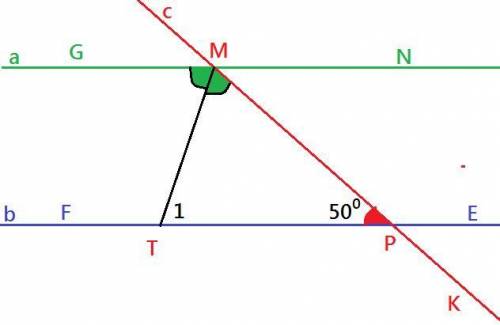
<PMN=<TPM=50° - как внутренние накрест лежащие углы при параллельных прямых а и b и секущей с.
<GMP и <PMN - смежные углы, их сумма 180°. => <GMP=180°-<PMN=180°-50°=130°
ТМ - биссектриса угла GMP. По свойству биссектрисы <GMT=<GMP/2=130/2=65°
<1=<GMT=65° - как внутренние накрест лежащие углы при параллельных прямых а и b и секущей MT.