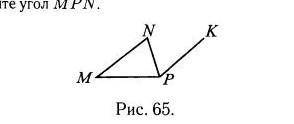
<MPK =180-30=150°
<MPN=<MPK/2=75°
Объяснение:
MPK =180-30=150°
<MPN=<MPK/2=75
Углы AOC и FOD равны как вертикальные. Треугольники CAO и DFO равны по стороне и прилежащим углам. В равных треугольниках против равных углов лежат равные стороны, CO=DO. Треугольники CBO и DEO равны по трем сторонам. В равных треугольниках против равных сторон лежат равные углы, ∠CBO=∠DEO.
AO=FO, ∠A=∠F (по условию), ∠AOC=∠FOD (вертикальные углы)
=> △CAO=△DFO (по стороне и прилежащим углам)
=> CO=DO (соответствующие стороны в равных треугольниках)
CB=DE, BO=EO (по условию)
=> △CBO=△DEO (по трем сторонам)
=> ∠CBO=∠DEO (соответствующие углы в равных треугольниках)
Объяснение:
Углы ∡1 и ∡2 ⇒ соответственные, значит они равны.
180° - 30° = 150° (∡MPK)
150° / 2 = 75° (∡MPN)
ответ: ∡MPN равен 75°