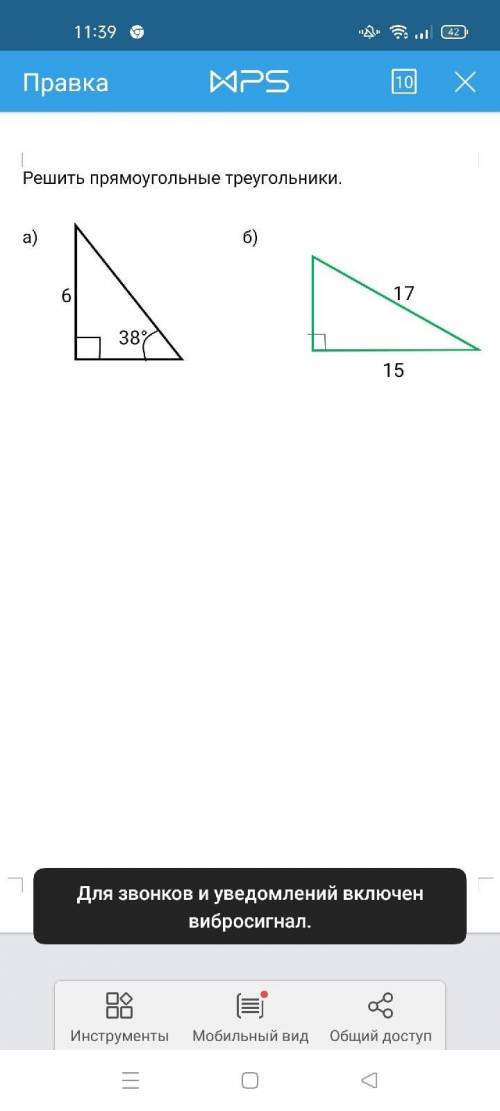
∆ АВС и ∆ МВС правильные, ВС - общая сторона. ⇒ эти треугольники равны, их стороны равны 2√3, их высоты равны. ⇒
МН=АН=2√3•sin60°=(2√3)•√3/2=3
Расстояние от точки до прямой - длина проведенного к прямой перпендикуляра - на рисунке в приложении это МК.
МК⊥АС⇒ проекция МК на плоскость ∆ АНС перпендикулярна АМ по обратной теореме о 3-х перпендикулярах.
Высота правильного треугольника есть его биссектриса ⇒
∆ АКН прямоугольный, катет НК противолежит углу 30° и равен половине АН
HK=1,5
В прямоугольном ∆ МНК по т.Пифагора гипотенуза
МК=√(MH²+KH²)=√(9+2,25)=1,5√5 - это ответ.
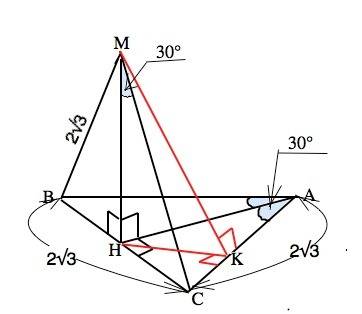
а) 9.746, 7.68, 6; 90°, 52°, 38°;
б) 17, 15, 8; 90°, 62°, 28°;
Объяснение: Для того чтобы решить треугольник нужно найти три стороны и три угла треугольника
а)
чтобы найти гипотенузу нужно противоположный катет поделить на синус данного угла: 6/sin(38°)=9.746;
чтобы найти второй катет нужно данный катет умножить на котангенс данного угла: 6*ctg(38°)=7.68;
В прямоугольном треугольнике чтобы найти угол между одним из его катетов и гипотенузой нужно 90 грудсов отнять другой угол между катетом и гипотенузой: 90°-38°=52°;
б)
Для того чтобы найти третью сторону нужно воспользоваться теоремой пифогора (a^2+b^2=c^2 => a=sqrt(c^2-b^2): sqrt(17^2-15^2)=8;
Находим углы за отношением прилегающих катетов к гипотенузе:
угол сверху (x-угол в градусах): cos(x)=8/17; x≈62°;
угол снизу (x-угол в градусах): cos(x)=15/17; x≈28°;
Для проверки добавим углы (они должны равнятся 90°, в противном случае это будет не треугольный треугольник и где-то была допущена ошибка: 28°+62°=90°