Объяснение:
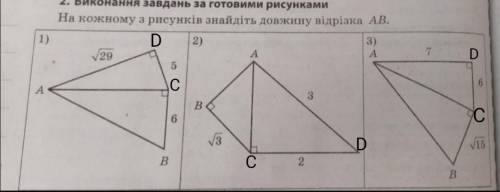
1)
∆ADC- прямоугольный.
По теореме Пифагора найдем гипотенузу
АС=√(AD²+DC²)=√(29+25)=√54.
∆ACB- прямоугольный.
По теореме Пифагора найдем гипотенузу
АВ=√(АС²+СВ²)=√(54+36)=√90=3√10
ответ: АВ=3√10
2)
∆АСD- прямоугольный.
По теореме Пифагора найдем катет
АС=√(AD²-CD²)=√(3²-2²)=√(9-4)=√5
∆ABC- прямоугольный.
По теореме Пифагора найдем катет
АВ=√(АС²-ВС²)=√(5-3)=√2
ответ: АВ=√2
3)
∆ADC- прямоугольный.
По теореме Пифагора найдем гипотенузу.
АС=√(АD²+DC²)=√(7²+6²)=√(49+36)=√85
∆ACB- прямоугольный.
По теореме Пифагора найдем гипотенузу
АВ=√(АС²+СВ²)=√(85+15)=√100=10
ответ: АВ=10
Так как по условию, точки М, К, Р середины отрезков АВ, ВД, ВС, то отрезок КМ средняя линия треугольника АВД, КР – средняя линия треугольника ВСД, МР – средняя линия треугольника АВС.
Отрезки средних линий параллельны основаниям треугольников: MK || АД, КР || СД, МР || АС, тогда и плоскость МКР параллельны плоскости АСД, что и требовалось доказать.
Длина средней линии треугольника равна половине длины параллельной стороны, тогда треугольник МКР подобен треугольнику АСД по трем пропорциональным сторонам с коэффициентом подобия К = АД / МК = АД / (АД / 2) = 2.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Sавс / Sмкр = 48 / Sмкр = 22.
Sмкр = 48 / 4 = 12 см2.
ответ: Площадь треугольника МКР равна 12 см2.