Вычисляем для начала длину медианы треугольника, обозначим её за m.
В правильном (равностороннем) треугольнике m=(√3/2)*a, где a- сторона треугольника.
m=(√3/2)*12=6√3 см
Далее воспользуемся следующим свойством медиан треугольника:
"Медианы треугольника пересекаются в одной точке (называемой центроидом), и делятся этой точкой на две части в отношении 2:1, считая от вершины"
Таким образом меньший участок медианы равен:
6√3/3=2√3
И теперь по теореме Пифагора находим нужное расстояние (рисунок уж я не стал делать...):
√((2√3)²+2²)=√(12+4)=√16=4 см
1) Т.к. углы CDB и CAB опираются на одну и ту же дугу, то они равны. Тогда треугольники DCB и ABC равны по стороне и 2-м углам(AC общая, а углы CDB=DBC=CAB=BAC т.к. треугольники DCB и ABC равнобедренные и углы CDB=CAB см. выше). Треугольники DCA и ABD равны по тому же принципу. В итоге треугольники CTB и DTA равнобедренные, а т.к. углы CTB и DTA вертикальные, то углы TDA и TBC равны, а это признак параллельности прямых, тогда CB || AD.
2) Пусть ACB=α. По формуле радиуса описанной окружности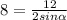 
, тогда 
. Угол DCA=180-3α. По теореме синусов имеем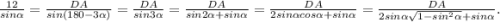 
. Теперь подставляем значение sinα=3/4 и вычисляем. У меня получилось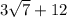 
Прикольная задача. Надеюсь, нигде не ошиблась.