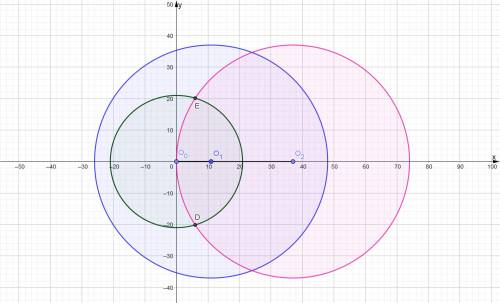
а)
У випадку, коли радіус першого кола R1 = 21 см і відстань до центру другого d = 11 см, інше коло має бути радіусом (R2) більшим або рівним 10 см ( |R1−d| ) і меншим за 32 ( |R1+d| ). Якщо виконується строга нерівність, то точок перетину буде дві; якщо виконується нестрога нерівність, точка перетину одна — дотична; якщо нерівність не виконується, друге коло не перетинає перше.
10 ≤ R2 ≤ 32
Коло з радіусом 37 в даний інтервал довжин не входить, нерівність не виконується ⇒ спільних точок немає.
б)
У випадку, коли радіус першого кола R1 = 21 см і відстань до центру другого d = 37 см, інше коло має бути радіусом (R2) більшим або рівним 16 см ( |R1−d| ) і меншим за 58 ( |R1+d| ). Якщо виконується строга нерівність, то точок перетину буде дві; якщо виконується нестрога нерівність, точка перетину одна — дотична; якщо нерівність не виконується, друге коло не перетинає перше.
16 ≤ R2 ≤ 58
Коло з радіусом 37 в даний інтервал довжин входить, нерівність строга ⇒ спільних точок дві.
нет
Объяснение:
Пусть диагонали пересекаются в точке О. Проверим, является ли она серединой для обоих этих отрезков:
О(х0; у0; z0)
{ (xA+xC)/2= xO
{ (yA+yC)/2= yO
{ (zA+zC)/2= zO
{ xO= (2+2)/2= 4/2= 2
{ yO= (6+2)/2=8/2= 4
{ zO= (4+3)/2= 7/2= 3,5
Итак, О(2; 4; 3,5)
Иначе
{ (xB+xD)/2= xO
{ (yB+yD)/2= yO
{ (zB+zD)/2= zO
{ xO= (0+1)/2= 1/2= 0,5
{ yO= (4+1)/2= 5/2= 2,5
{ zO= (3+1)/2= 4/2= 2
Получили О(0,5; 2,5; 2). Очевидно, что середины диагоналей не совпадают, то есть точкой пересечения они НЕ делятся пополам. Данный четырехугольник ABCD не является параллелограммом.
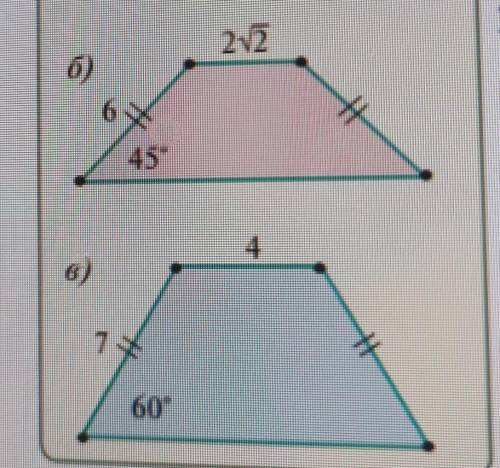
а)
∆АВМ- прямоугольный равнобедренный треугольник. Углы при основании равны 45°.
АМ=ВМ.
АМ=АВ/√2=6/√2=3√2 ед.
BM=3√2ед
МН=ВС=2√2ед
АD=2*AM+MH=2*3√2+2√2=8√2ед.
S(ABCD)=BM(ВС+АD)/2=
=3√2(2√2+8√2)/2=3√2*10√2/2=30ед²
ответ: 30ед²
б)
∆LMH- прямоугольный треугольник
LH- катет против угла <LMH=30°
LH=LM/2=7/2=3,5 ед.
LK=2*LH+MN=2*3,5+4=11ед.
По теореме Пифагора
МН=√(LM²-LH²)=√(7²-3,5²)=3,5√3 ед.
S(LMNK)=MH(MN+LK)/2=3,5√3(4+11)/2=
=3,5√3*15/2=26,25√3 ед²
ответ: 26,25√3 ед²