В равнобедренном треугольнике ABC рассмотрим два треугольника KAC и MCA. Треугольник KAC равен треугольнику MCA по двум сторонам и углу между ними, а именно:
1). Сторона AC - общая;
2). MA=KC, так как:
AB=BC, ведь треугольник ABC - равнобедренный, а MA=1/2*AB (т. M - середина AB, т.к. MC - медиана), KC=1/2*BC (т. K - середина BC, т.к. KA - медиана), значит MA=KC;
3). ∠BAC=∠BCA, т.к. треугольник ABC - равнобедренный.
Из равенства треугольников KAC и MCA следует равенство соответственных элементов, а значит ∠KAC=∠MCA, что и требовалось доказать.
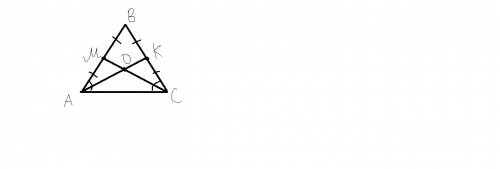
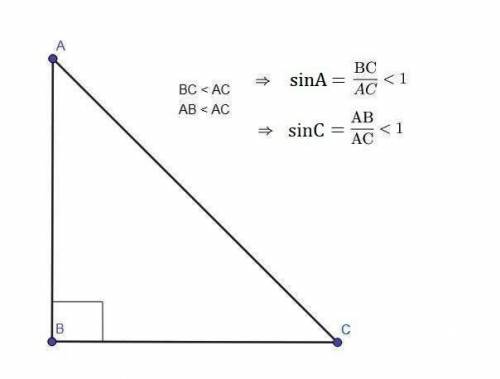
Для начала вспомним, что такое синус острого угла прямоугольного треугольника.
Синус острого угла прямоугольного треугольника - это отношение противолежащего катета к гипотенузе.
Из курса седьмого класса мы знаем, что гипотенуза - это самая большая сторона в прямоугольном треугольнике, она всегда больше любого катета.
Из курса математики мы знаем, что если числитель (в числителе стоит длина катета) меньше знаменателя (в знаменателе стоит длина гипотенузы), то дробь меньше единицы.
То есть, та самая дробь (значение синуса острого угла) меньше единицы.
(Кстати, синус острого угла также больше нуля, так как числитель и знаменатель положительного знака. Это связано с тем, что длина сторон не может выражаться отрицательными числами).
Твтатаьпьптьбопвсстпамт не спамни